Python-Kurs

Numerische Operationen auf NumPy-Arrays

In unserem Python-Tutorial haben wir viele Operatoren gesehen. Darüber haben wir dort gelernt, wie man Operatoren mittels "magischer Funktionen" überladen kann. Wir wissen nun, dass wir beispielsweise das "+"-Operatorzeichen nutzen können, um numerische Werte zu addieren oder Strings und Listen zu konkatenieren:

42 + 5

"Python ist eine der besten " + "oder die beste Programmiersprache!"

In dieser Einführung werden wir nun lernen, dass auch in NumPy die Operatorzeichen entsprechend überladen sind, sodass wir sie in "natürlicher" Weise nutzen können.

So können wir beispielsweise Skalare zu Arrays addieren, d.h. der Skalar wird zu jeder Komponente addiert. Das Gleiche ist möglich für die Subtraktion, die Division, die Multiplikation und sogar für Funktionen wie Sinus, Kosinus und so weiter.

Selbstverständlich können wir auch all diese Operatoren auf zwei Arrays anwenden.

Operatoren und Skalare

Beginnen wir mit der skalaren Addition:

Multiplikation, Subtraktion, Division und Exponentiation sind ebenso leicht zu bewerkstelligen wie die vorige Addition:

Wir hatten dieses Beispiel mit einer Liste lst begonnen. Wie kann man zu einer numerischen Liste einen Skalar addieren, so wie wir es mit dem Array v getan hatten?

Zu diesem Zweck kann man natürlich eine for-Schleife nutzen. Im folgenden addieren wir 2 zu den Werten dieser Liste:

Obwohl diese Lösung funktioniert, ist sie nicht elegant und pythonisch. Zu diesem Zweck nutzt man besser eine Listenabstraktion (englisch: list comprehension) statt der umständlichen Lösung mit for-Schleife. Wir empfehlen unser Kapitel über Listenabstraktion unseres Python-Tutorials, falls jemand mit der Thematik nicht oder nicht mehr vertraut sein sollte.

Obwohl wir bereits einen Zeitvergleich zwischen NumPy und reinem Python durchgeführt hatten, wollen wir dennoch auch diese beiden Ansätze vergleichen:

Arithmetische Operationen auf zwei Arrays

Falls wir ein weiteres Array statt einem Skalar benutzen, werden die Elemente von beiden Arrays komponentenweise miteinander verknüpft.

Das Array verzehr_in_gramm enthält den Verzehr einer fiktiven Person, die genauestens über ihren Esskonsum buchführt. Die Kalorienaufnahme pro Lebensmittel können wir dann mittels einer komponentenweisen Multiplikation mit dem Array bestimmen:

A * B im vorigen Beispiel sollte keinesfalls mit der Matrizenmultiplikation verwechselt werden. Wie bereits gesagt werden in unserem Beispiel die Arrays nur komponentenweise multipliziert!

Matrizenmultiplikation und Skalarprodukt

Definition der dot-Funktion

In englischen Texten wird häufig bei dieser NumPy-Funktionalität vom "dot product" gesprochen. Mathematisch versteht man unter dem "dot product" das Skalarprodukt oder "innere Produkt" von zwei Vektoren. Seltener wird auch die Bezeichnung "Punktprodukt", also die wörtliche Übersetzung von "dot product", für das Skalarprodukt verwendet. Da das Skalar- oder Punktprodukt in der Mathematik üblicherweise nur für den eindimensionalen Fall bei Vektoren definiert ist und die dot-Funktion von NumPy aber auf beliebige Funktionen angewendet werden kann, sprechen wir von dot-Funktion, um Verwechslungen zur Mathematik vorzubeugen.

Die Syntax der dot-Funktion sieht wie folgt aus:

dot(a, b, out=None)

Die Funktion dot liefert das dot-Produkt von a und b zurück.

Falls sowohl a als auch b Skalare sind oder beide eindimensionale Arrays, wird ein Skalar zurückgegeben, ansonsten ein Array.

Für eindimensionale Arrays entspricht es dem Skalarprodukt, auch inneres Produkt genannt, von Vektoren, jedoch ohne komplexe Konjugation.

Für zweidimensionale Arrays entspricht das dot-Produkt der Matrizenmultiplikation.

Für N Dimensionen wird das Summenprodukt über die letzte Achse von a und die vorletzte Achse von b gebildet.

Diesen Fall werden wir im Folgenden noch an Beispielen verdeutlichen.

Die Funktion erhebt einen ValueError, falls die Shape der letzten Dimension von a nicht die gleiche Größe wie die Shape der zweitletzten Dimension von b hat, d.h. es muss gelten a.shape[-1] == b.shape[-2].

Beispiele zur dot-Funktion

Wir beginnen mit den Fällen, in denen beide Argumente Skalare oder eindimensionale Arrays sind:

Im zweidimensionalen Fall realisiert die dot-Funktion die Matrizenmultiplikation. Betrachten wir dazu folgendes Beispiel

Seit Python 3.5 gibt es für das dot-Produkt auch einen Infix-Operator, und zwar @:

Damit die Matrizenmultiplikation (also dot) für zwei Matrizen A und B im zweidimensionalen Fall funktionieren kann, muss gelten:

A.shape[-1] == B.shape[-2]

Aus dem vorigen Beispiel können wir lernen, dass die Anzahl der Spalten des ersten zweidimensionalen Arrays gleich der Anzahl der Zeilen des zweiten zweidimensionalen Arrays sein muss.

Das dot-Produkt im 3-dimensionalen Fall

Es wird ziemlich verzwickt, wenn wir 3-dimensionale Arrays als Argumente von dot benutzen.

Im ersten Beispiel benutzen wir zwei symmetrische 3-dimensionale Arrays:

Nun betrachten wir das Produkt von zwei nicht-symmetrischen dreidimensionalen Arrays:

Die Funktion squeeze erlaubt uns, Dimensionen zu schrumpfen, indem eindimensionale Einträge aus der shape eines Arrays entfernt werden. Wir zeigen dies an einem einfachen Beispiel:

Nun wenden wir squeeze auf das Array R an, um die Shape von (3, 3, 1, 3) auf (3, 3, 3) zu schrumpfen:

Um zu zeigen, wie das dot-Produkt im dreidimensionalen Fall funktioniert, werden wir jedoch nun zwei nicht-symmetrische dreidimensionale Arrays im folgenden Beispiel benutzen:

Schauen wir uns nun die folgenden Summen-Produkte an:

Hoffentlich ist Ihnen aufgefallen, dass die Werte, die wir erzeugt haben, den Elementen von R[0] entsprechen:

Dies bedeutet, dass wir das Array R auch über die Summen-Produkte hätten erzeugen können. Um dies zu "beweisen", werden wir im folgenden Beispiel ein Array R2 unter Benutzung der Summen-Produkte erzeugen. Anschließend prüfen wir, ob R2 gleich R ist.

Es gilt also, was wir eingangs behauptet haben:

dot(X, Y)[i,j,k,m] = sum(X[i,j,:] * Y[k,:,m])

Vergleichsoperatoren

Wir kennen bereits Vergleichsoperatoren in Python, die wir auf Integer, Floats oder Strings angewendet haben. Sie liefern True oder False zurück. Vergleichen wir zwei Arrays miteinander, erhalten wir keinen "einfachen" Booleschen Wert zurück. Die Vergleiche werden elementweise durchgeführt. Dies bewirkt, dass wir ein Boolesches Array als Rückgabewert erhalten:

Man kann aber auch Arrays vollständig auf Gleichheit überprüfen. Dazu benutzen wir die Funktion array_equal, die True zurückliefert, falls zwei Arrays die gleiche Shape haben und alle Elemente gleich sind. Ansonsten wird False zurückgeliefert.

Logische Operatoren

Wir können Arrays auch komponentenweise auf ein logisches 'oder' und ein logisches 'und' vergleichen. Dazu gibt es die Funktionen logical_or und logical_and.

Broadcasting

Bisher gingen wir davon aus, dass Arrays die gleiche Shape haben müssen, damit wir numerische Operatoren auf diese anwenden können. Unter dem Namen "Broadcasting" stellt NumPy einen mächtigen Mechanismus zur Verfügung, der es erlaubt, arithmetische Operatoren auch auf Arrays mit unterschiedlicher Shape anzuwenden. Um die entsprechende Operation durchzuführen, wird nun das "kleinere" Array entweder in eine "passende Form" transformiert oder mehrmals auf das "größere" angewendet. In anderen Worten: Unter bestimmten Bedingungen erfolgt ein "Broadcast" des kleineren Arrays, bis es die gleiche Shape wie das größere hat.

Mit Hilfe des Broadcasting können wir Schleifen in unseren Python-Programmen vermeiden. Die Schleifenbildung erfolgt dann implizit in der NumPy-Implementierung, d.h. in C. Dadurch vermeiden wir außerdem unnötige Kopien von unseren Daten.

Prinzipiell gibt es drei verschiedene Formen von Broadcasting:

• in horizontaler Richtung
• in vertikaler Richtung
• in horizontaler und vertikaler Richtung

Broadcasting bei zwei Arrays in NumPy erfolgt nach folgenden Regeln:

Regel 1

Falls die beiden Arrays in ihrer Anzahl von Dimensionen sich unterscheiden, wird die Shape des Arrays, das weniger Dimensionen hat, mit Einsen von der linken Seite aus
aufgefüllt.

Regel 2

Falls die Shapes von zwei Arrays an einer Shape-Position nicht übereinstimmen, wird die Shape desjenigen Arrays angepasst, die eine 1 enthält. Der Wert wird dann auf den Wert des anderen Arrays erhöht.

Regel 3

Falls in irgendeiner Dimension die Größen unterschiedlich sind und keine von beiden gleich 1 ist, wird ein Fehler erhoben.

Im Folgenden werden wir klarer sehen, was die Anwendung dieser Regeln bewirken.

Einen besonders einfachen Fall von Broadcasting haben wir schon kennengelernt. Der einfachste Fall ist die Skalarenmultiplikation:

Statt einem Skalar für x hätte man auch den Vektor np.array([4, 4, 4]) nehmen können und hätte das gleiche Ergebnis erhalten:

Normalerweise denkt man aber nicht an diesen Fall, wenn man von Broadcasting spricht.

Zeilenweises Broadcasting

Betrachten wir die beiden Arrays A und B und ihre Shapes:

Das folgende Diagramm illustriert die Arbeitsweise von Broadcasting:

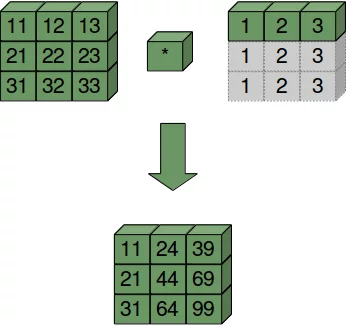
B wird benutzt, als wäre es wie folgt aufgebaut:

"Zeilenweise" bedeutet also, dass wir ein eindimensionales Array als die zu broadcastende Zeile betrachten.

Broadcasting funktioniert auch bei höheren Dimensionen, solange sich die beiden ersten Regeln erfolgreich anwenden lassen. Wir demonstrieren dies im folgenden Beispiel:

Auch in diesem Falle wollen wir uns anschauen, was man machen müsste, um das Broadcasting nach den Regeln zu simulieren:

Spaltenweises Broadcasting:

In diesem Fall haben wir wieder ein eindimensionales Array, betrachten es nun aber als Spaltenvektor des Broadcast-Arrays.

Für dieses Beispiel müssen wir wissen, wie man einen Zeilenvektor in einen Spaltenvektor wandelt. Hierzu gibt es zwei Möglichkeiten. Mittels reshape:

Alternativ können wir auch newaxis verwenden:

Nun können wir die Multiplikation mittels Broadcasting durchführen:

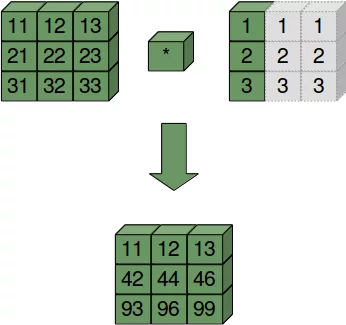
B wird benutzt als wäre es wie folgt aufgebaut:

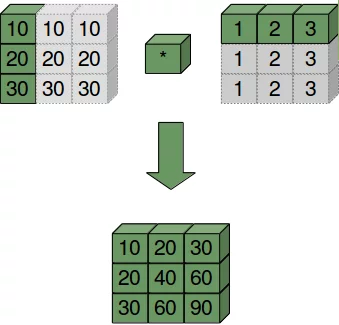
Broadcasting von zwei eindimensionalen Arrays

Nun betrachten wir den Fall, dass wir zwei eindimensionale Arrays verknüpfen möchten. Den ersten wollen wir als Spaltenvektor betrachten und den zweiten als Zeilenvektor. Im Prinzip kombinieren wir nun die Verfahren der beiden vorigen Fälle, also spaltenweises und zeilenweises Broadcasting:

Distanzmatrix

In der Mathematik, der Informatik und insbesondere in der Graph-Theorie, versteht man unter der Distanzmatrix ein zweidimensionales Array, das die "Entfernungen" zwischen den Elementen einer Menge paarweise beinhaltet. Die Größe dieses zweidimensionalen Arrays ist n x n, falls die Menge aus n Elementen besteht.

Ein praktisches Beispiel einer Distanzmatrix ist eine Matrix mit den Entfernungen zwischen geografischen Lokationen, in unserem Beispiel europäische Städte:

Ufuncs

Bisher haben wir diverse Operatoren wie Addition, Subtraktion, Multiplikation und so weiter für Arrays kennengelernt. Allen sind bestimmte Features gemeinsam, wie Broadcasting und erzwungene Typumwandlung (englisch: type coercion). Allen Operationen ist auch die elementweise Anwendung gemeinsam.

Zu den bereits kennengelernten Infix-Operatoren wie $+$, $-$, $*$ und so weiter gibt es auch Funktionen wie add, subtract, multiply, divide, remainder, power und weitere. Aber es gibt auch Funktionen, für die es keine Infix-Variante gibt, da es sich um Funktionen handelt, die nur ein Argument erwarten, also unäre Operatoren: arccos, arccosh, arcsin, arcsinh, arctan, arctanh, cos, cosh, tan, tanh, log10, sin, sinh, sqrt, absolute, fabs, floor, ceil, fmod, exp, log, conjugate, maximum, minimum.

Auch für die Infix-Vergleichsoperatoren <, <=, ==, >, >=, != und so weiter gibt es entsprechende funktionale Varianten: greater, greater_equal, equal, less, less_equal, not_equal, logical_or, logical_xor, logical_not, logical_and, bitwise_or, bitwise_xor, bitwise_not, bitwise_and, rshift, lshift

Diese Funktionen bezeichnet man als Ufuncs, auch als universelle Funktionen bekannt.

Anwendung von Ufuncs

Die funktionalen und Infix-Varianten sind äquivalent.

Die Ufuncs lassen sich auf beliebige Python-Sequenzen anwenden, sofern sie aus numerischen Datentypen bestehen und bezüglich ihrer Längen und Shapes übereinstimmen:

Die unären Ufunc-Funktionen können sowohl auf NumPy-Arrays als auch auf andere Python-Sequenzen angewendet werden. Der Rückgabewert ist aber in allen Fällen ein numpy.ndarray-Wert:

Sie können auch auf Instanzen der int- und float-Klassen aufgerufen werden. Rückgabewerte sind in diesen Fällen numpy.int64- bzw. numpy.float64-Typen:

Parameter für Rückgabewerte bei Ufuncs

Eine weitere Besonderheit der Ufuncs besteht darin, dass ihnen auch ein Parameter für das Rückgabeobjekt übergeben werden kann. Betrachten wir dazu das folgende Beispiel:

In den obigen Fällen wurde zuerst ein neues ndarray-Array mit dem Ergebnis erzeugt und dann wurde dieses Array der Variablen x zugewiesen. Das alte Array wird danach nicht mehr benötigt und muss gelöscht werden.

Indem wir die Variable x als Rückgabeparameter spezifizieren, wird die Operation in-place durchgeführt, also effizienter:

Die in-place-Variante mit Rückgabeparameter ist im Allgemeinen deutlich schneller, aber nicht immer, wie wir im Folgenden sehen können:

accumulate

Auf die Ufunc-Funtionen kann die accumulate-Methode angewendet werden.

Die accumulate-Funktion bewirkt die Anwendung des Operators auf alle Elemente des Arrays und der darauffolgenden Akkumulation der Ergebnisse.

Wendet man accumulate auf die add-Funktion an, erhält man eine zu np.cumsum äquivalente Funktionalität, wie wir im folgenden Beispiel demonstrieren.

Den mehrdimensionalen Fall und die Benutzung des optionalen Parameters axis verdeutlichen wir mit folgendem selbsterklärenden Beispiel:

reduce

Die Arbeitsweise von reduce im eindimensionalen Fall, kann wie folgt beschreiben werden:

Nehmen wir an, op ist eine Funktion wie numpy.add oder numpy.multiply. Wendet man op.reduce auf ein Objekt x an, welches eine numerische Python-Sequenz oder ein eindimensionales Array sein kann, so liefert sie einen einzelnen Wert zurück. Die Berechnung geschieht wie folgt: Falls x leer ist, wird 0.0 zurückgeliefert. Besitzt x nur ein Element, wird dieses als Ergebnis von op.reduce(x) zurückgeliefert. Bei mehr als einem Element in x wird op zuerst auf die ersten beiden Elemente von x angewendet. Gibt es noch weitere Elemente, wird op auf dieses Ergebnis und auf das folgende Element von x angewendet. Dies wird solange fortgesetzt, bis es keine weiteren Elemente mehr gibt, und das letzte Ergebnis wird dann als Gesamtergebnis zurückgeliefert:

Im mehrdimensionalen Fall bewirkt die Anwendung von reduce die Reduktion um eine Dimension. Eine Reduktion über alle Dimensionen erhält man, indem man axis auf None setzt:

outer

op.outer(A, B) bewirkt, dass op auf alle Paare (a, b) mit a in A und b in B angewendet wird.

In der Mathematik ist dieses spezielles Produkt zweier Vektoren auch als das "dyadische Produkt" oder "tensorielle Produkt" bekannt. Das Ergebnis ist eine Matrix.

at

at(a, indices, b=None) führt eine ungepufferte in-place-Operation auf den durch indices spezifizierten Indizes von a durch. Für die Addition ist dies beispielsweise äquivalent mit a[indices] += b, außer dass die Elemente, die mehrfach indiziert sind, akkumuliert werden.