# invisible
lines = open("img_resolution.txt").readlines()
resolution = lines[0].strip()
if resolution != "default":
import matplotlib as mpl
mpl.rcParams['figure.dpi'] = int(resolution)
Matplotlib Tutorial: Legenden und Kommentare hinzufügen¶
Legende hinzufügen¶

Wenn wir uns die Linien-Graphen der vorigen Beispiele anschauen, dann merken wir, dass wir uns immer den Code anschauen müssen, um zu verstehen, welche Art von Funktion dargestellt wird. Diese Information sollte der Einfachheit halber direkt im Diagramm erscheinen. Dafür werden Legenden verwendet. Der Begriff stammt aus dem Lateinischen und steht für "das, was zu lesen ist". Also was gelesen werden muss, um den Graphen zu verstehen.
Bevor Legenden in mathematischen Graphen Verwendung fanden, wurden sie auf Karten verwendet. Legenden -- wie sie auf Karten zu finden waren -- haben die Bildsprache oder Symbolik auf der Karte erläutert. Auf Graphen erläutern sie die Funktion oder die Werte, die hinter den verschiedenen Linien des Graphen liegen.
Im Folgenden demonstrieren wir ein einfaches Beispiel, wie eine Legende auf dem Graphen platziert werden kann. Eine Legende enthält einen oder mehrere Einträge. Jeder Eintrag besteht aus einem Schlüssel und einer Beschriftung.
Die pyplot-Funktion legend(*args, **kwargs) platziert eine Legende im Plot.
Alles, was wir tun müssen, um eine Legende für Linien zu erstellen, die bereits im Plot existieren, ist der einfache Aufruf der Funktion legend mit einem iterierbaren Array aus Strings. Eins für jedes Element der Legende. Zum Beispiel:
import numpy as np
import matplotlib.pyplot as plt
ax = plt.gca()
ax.plot([1, 2, 3, 4])
ax.legend(['A simple line'])
plt.show()
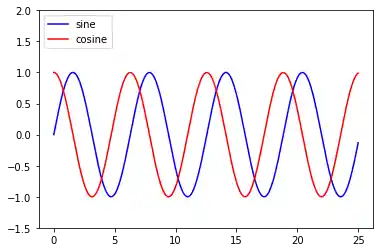
Wenn wir eine Beschriftung hinzufügen, um die Funktion zu zeichnen (plotten), wird der Wert automatisch als Beschriftung im legend-Kommando verwendet. Das einzige Argument, welches die legend-Funktion braucht, ist das Positions-Argument loc:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 25, 1000)
y1 = np.sin(x)
y2 = np.cos(x)
plt.plot(x, y1, '-b', label='sine')
plt.plot(x, y2, '-r', label='cosine')
plt.legend(loc='upper left')
plt.ylim(-1.5, 2.0)
plt.show()
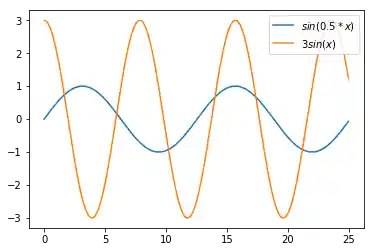
Es folgt nun ein Beispiel mit der Legende in der rechten oberen Ecke:
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(0, 25, 1000)
F1 = np.sin(0.5 * X)
F2 = 3 * np.cos(0.8*X)
plt.plot(X, F1, label="$sin(0.5 * x)$")
plt.plot(X, F2, label="$3 sin(x)$")
plt.legend(loc='upper right')
plt.show()
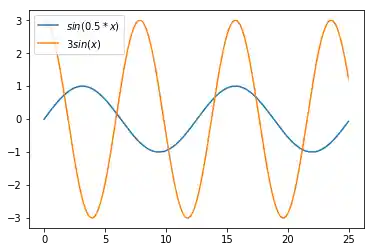
In den meisten Fällen weiß man jedoch nicht, wie das Ergebnis aussehen wird, bevor es nicht ausgegeben wurde. Möglicherweise könnte die Legende einen wichtigen Teil des Plots überdecken. Wenn Sie nicht wissen, wie die Daten aussehen werden, können Sie best als Argument für loc verwenden. Matplotlib wird automatisch versuchen, die bestmögliche Position für die Legende zu finden:
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(0, 25, 1000)
F1 = np.sin(0.5 * X)
F2 = 3 * np.cos(0.8*X)
plt.plot(X, F1, label="$sin(0.5 * x)$")
plt.plot(X, F2, label="$3 sin(x)$")
plt.legend(loc='best')
plt.show()
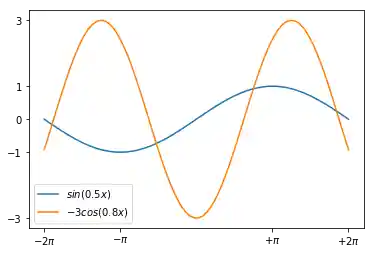
In den folgenden beiden Beispielen kann man sehen, dass loc='best' sehr gut funktioniert:
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(-2 * np.pi, 2 * np.pi, 70, endpoint=True)
F1 = np.sin(0.5*X)
F2 = -3 * np.cos(0.8*X)
plt.xticks( [-6.28, -3.14, 3.14, 6.28],
[r'$-2\pi$', r'$-\pi$', r'$+\pi$', r'$+2\pi$'])
plt.yticks([-3, -1, 0, +1, 3])
plt.plot(X, F1, label="$sin(0.5x)$")
plt.plot(X, F2, label="$-3 cos(0.8x)$")
plt.legend(loc='best')
plt.show()
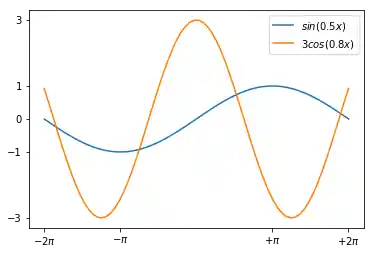
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(-2 * np.pi, 2 * np.pi, 70, endpoint=True)
F1 = np.sin(0.5*X)
F2 = 3 * np.cos(0.8*X)
plt.xticks( [-6.28, -3.14, 3.14, 6.28],
[r'$-2\pi$', r'$-\pi$', r'$+\pi$', r'$+2\pi$'])
plt.yticks([-3, -1, 0, +1, 3])
plt.plot(X, F1, label="$sin(0.5x)$")
plt.plot(X, F2, label="$3 cos(0.8x)$")
plt.legend(loc='best')
plt.show()
Kommentare¶
Natürlich hat die Sinus-Funktion "langweilige" und "interessante" Werte. Nehmen wir an, dass uns speziell der Wert von
$3 * sin(3 * pi/4)$
interessiert.
import numpy as np
print(3 * np.sin(3 * np.pi/4))
Der Zahlenwert sieht nicht sehr speziell aus. Wenn wir aber eine symbolische Berechnung durchführen, resultiert daraus $\frac{3}{\sqrt{2}}$.
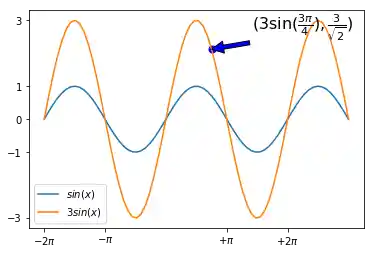
Jetzt möchten wir genau diesen Punkt auf dem Graph markieren. Dies erreichen wir mit der Funktion annotate.
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(-2 * np.pi, 3 * np.pi, 70, endpoint=True)
F1 = np.sin(X)
F2 = 3 * np.sin(X)
ax = plt.gca()
plt.xticks( [-6.28, -3.14, 3.14, 6.28],
[r'$-2\pi$', r'$-\pi$', r'$+\pi$', r'$+2\pi$'])
plt.yticks([-3, -1, 0, +1, 3])
x = 3 * np.pi / 4
# mit scatter kann man einen einzelnen Punkt erzeugen:
plt.scatter([x,],[3 * np.sin(x),], 50, color ='blue')
# Die in annotate verwendete Notation kommt von LaTeX:
plt.annotate(r'$(3\sin(\frac{3\pi}{4}),\frac{3}{\sqrt{2}})$',
xy=(x, 3 * np.sin(x)),
xycoords='data',
xytext=(+40, +20),
textcoords='offset points',
fontsize=16,
arrowprops=dict(facecolor='blue'))
plt.plot(X, F1, label="$sin(x)$")
plt.plot(X, F2, label="$3 sin(x)$")
plt.legend(loc='lower left')
plt.show()
Dafür mussten wir der annotate-Funktion einige Informationen als Parameter bereitstellen.
| Parameter | Bedeutung |
|---|---|
| xy | Koordinaten der Pfeilspitze |
| xytext | Koordinaten der Text-Position |
Die xy- und xytext-Positionen sind in unserem Beispiel in den Daten-Koordinaten enthalten. Es gibt weitere Koordinaten-Systeme, aus denen wir wählen können. Das Koordinaten-System von xy und xytext kann über String-Werte mit xycoords und textcoords spezifiziert werden. Der Default-Wert ist "data":
| String-Wert | Koordinaten-System |
|---|---|
| figure points | Punkte von der linken unteren Ecke der Abbildung |
| figure pixels | Pixel von der linken unteren Ecke der Abbildung |
| figure fraction | 0,0 ist links unten und 1,1 ist rechts oben in der Abbildung |
| axes points | Punkte von der linken unteren Ecke der Achsen |
| axes pixels | Pixel von der linken unteren Ecke der Achsen |
| axes fraction | proportionaler Anteil, 0,0 ist links unten und 1,1 ist rechts oben |
| data | Verwende das Achsen-Daten-Koordinaten-System |
Zusätzlich können die Eigenschaften des Pfeils spezifiziert werden. Dafür müssen wir ein Dictionary mit Pfeil-Eigenschaften als Parameter arrowprops bereitstellen:
| arrowprops Schlüssel | Beschreibung |
|---|---|
| width | Die Breite des Pfeils in Punkten |
| headlength | Der Teil, der vom Pfeilkopf eingenommen wird. |
| headwidth | Die Breite der Pfeilspitzen-Basis in Punkten |
| shrink | Verschiebe die Spitze und Basis um ein paar Prozent vom Kommentar-Punkt und -Text |
| **kwargs | ein Schlüssel für matplotlib.patches.Polygon, z.B. facecolor |
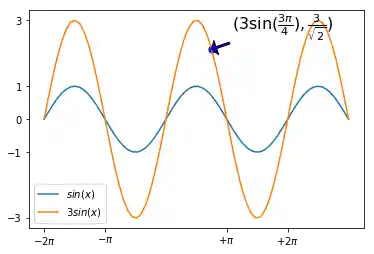
Im folgenden Beispiel verändern wir das Erscheinungsbild des Pfeils aus unserem vorigen Beispiel:
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(-2 * np.pi, 3 * np.pi, 70, endpoint=True)
F1 = np.sin(X)
F2 = 3 * np.sin(X)
ax = plt.gca()
plt.xticks( [-6.28, -3.14, 3.14, 6.28],
[r'$-2\pi$', r'$-\pi$', r'$+\pi$', r'$+2\pi$'])
plt.yticks([-3, -1, 0, +1, 3])
x = 3 * np.pi / 4
plt.scatter([x,],[3 * np.sin(x),], 50, color ='blue')
plt.annotate(r'$(3\sin(\frac{3\pi}{4}),\frac{3}{\sqrt{2}})$',
xy=(x, 3 * np.sin(x)),
xycoords='data',
xytext=(+20, +20),
textcoords='offset points',
fontsize=16,
arrowprops=dict(facecolor='blue',
headwidth=15,
headlength=5,
width=2))
plt.plot(X, F1, label="$sin(x)$")
plt.plot(X, F2, label="$3 sin(x)$")
plt.legend(loc='lower left')
plt.show()


 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen