# invisible
import numpy as np
np.core.arrayprint._line_width = 65

Wir haben bereits im vorigen Kapitel unseres NumPy-Tutorials gesehen, dass wir NumPy-Arrays aus Listen und Tupel generieren können. Nun wollen wir weitere Funktionen zum Erzeugen von Arrays einführen.
NumPy bietet Funktionen, um Intervalle mit Werten zu erzeugen, deren Abstände gleichmäßig verteilt sind. arange benutzt einen gegebenen Abstandwert, um innerhalb von gegebenen Intervallgrenzen entsprechende Werte zu generieren, während linspace eine bestimmte Anzahl von Werten innerhalb gegebener Intervallgrenzen berechnet. Den Abstand berechnet linspace automatisch.
Erzeugung äquidistanter Intervalle
arange
Die Syntax von arange:
arange([start,] stop[, step], [, dtype=None])
arange liefert gleichmäßig verteilte Werte innerhalb eines gegebenen Intervalles zurück. Die Werte werden innerhalb des halb-offenen Intervalles [start, stop) generiert. Wird diese Funktion mit Integer-Werten benutzt, ist sie beinahe äquivalent zu der built-in Python-Funktion range.
arange liefert jedoch ein ndarray zurück, während range einen Listen-Iterator zurückliefert.
Falls der start-Parameter nicht übergeben wird, wird start auf 0 gesetzt.
Das Ende des Intervalls wird durch den Parameter stop bestimmt. Üblicherweise wird das Intervall diesen
Wert nicht beinhalten, außer in den Fällen, in denen step keine Ganzzahl ist und floating-point-Effekte
die Länge des Ausgabearrays beeinflussen. Der Abstand zwischen zwei benachbarten Werten des Ausgabearrays kann mittels des optionalen Parameters step gesetzt werden. Der Default-Wert für step ist 1.
Falls ein Wert für step angegeben wird, kann der start-Parameter nicht mehr optional sein, d.h. er muss dann auch angegeben werden.
Der Type des Ausgabearrays kann mit dem Parameter dtype bestimmt werden. Wird er nicht angegeben, wird der Typ automatisch aus den übergebenen Eingabewerten ermittelt.
import numpy as np
a = np.arange(1, 7)
print(a)
# im Vergleich dazu nun range:
x = range(1, 7)
print(x) # x ist ein Iterator
print(list(x))
# weitere arange-Beispiele:
x = np.arange(7.3)
print(x)
x = np.arange(0.5, 6.1, 0.8)
print(x)
x = np.arange(0.5, 6.1, 0.8, int)
print(x)
linspace
Die Syntax von linspace:
linspace(start, stop, num=50, endpoint=True, retstep=False)
linspace liefert ein ndarray zurück, welches aus 'num' gleichmäßig verteilten Werten
aus dem geschlossenen Interval ['start', 'stop'] oder dem halb-offenen Intervall ['start', 'stop') besteht. Ob ein geschlossenes oder ein halb-offenes Intervall zurückgeliefert wird,
hängt vom Wert des Parameters endpoint ab. stop ist der letzte Wert des Intervalls, falls endpoint
nicht auf False gesetzt ist. Die Schrittweite ist unterschiedlich, je nachdem, ob endpoint True oder False ist:
import numpy as np
# 50 Werte (Defaut) zwischen 1 und 10:
print(np.linspace(1, 10))
# 7 Werte zwischen 1 und 10:
print(np.linspace(1, 10, 7))
# jetzt ohne Endpunkt:
print(np.linspace(1, 10, 7, endpoint=False))
Bis jetzt haben wir einen interessanten Parameter nicht besprochen. Falls der Parameter 'retstep' gesetzt ist, wird die Funktion auch den Wert des Abstandes zwischen zwei benachbarten Werten des Ausgabearrays zurückliefern. Die Funktion liefert also ein Tupel ('samples', 'step') zurück:
import numpy as np
samples, spacing = np.linspace(1, 10,
retstep=True)
print(spacing)
samples, spacing = np.linspace(1, 10, 5,
endpoint=True, retstep=True)
print(samples, spacing)
samples, spacing = np.linspace(1, 10, 5,
endpoint=False, retstep=True)
print(samples, spacing)
Nulldimensionale Arrays in NumPy
In NumPy kann man mehrdimensionale Arrays erzeugen. Skalare sind 0-dimensional. Im folgenden Beispiel erzeugen wir den Skalar 42. Wenden wir die ndim-Methode auf unseren Skalar an, erhalten wir die Dimension des Arrays. Wir können außerdem sehen, dass das Array vom Typ numpy.ndarray ist.
import numpy as np
x = np.array(42)
print("x: ", x)
print("Der Typ von x: ", type(x))
print("Die Dimension von x:", np.ndim(x))
Eindimensionales Array
Wir haben bereits in unserem anfänglichen Beispiel ein eindimensionales Array -- besser als Vektoren bekannt -- gesehen. Was wir bis jetzt noch nicht erwähnt haben, aber was Sie sich sicherlich bereits gedacht haben, ist die Tatsache, dass die NumPy-Arrays Container sind, die nur einen Typ enthalten können, also beispielsweise nur Integers. Den homogenen Datentyp eines Arrays können wir mit dem Attribut dtype bestimmen, wie wir im folgenden Beispiel lernen können:
F = np.array([1, 1, 2, 3, 5, 8, 13, 21])
V = np.array([3.4, 6.9, 99.8, 12.8])
print("F: ", F)
print("V: ", V)
print("Typ von F: ", F.dtype)
print("Typ von V: ", V.dtype)
print("Dimension von F: ", np.ndim(F))
print("Dimension von V: ", np.ndim(V))
A = np.array([ [3.4, 8.7, 9.9],
[1.1, -7.8, -0.7],
[4.1, 12.3, 4.8]])
print(A)
print(A.ndim)
Dreidimensionale Arrays werden wir uns in einem späteren Kapitel genauer anschauen.
Shape/Gestalt eines Arrays
Die Funktion shape liefert die Größe bzw. die Gestalt eines Arrays in Form eines Integer-Tupels zurück. Diese Zahlen bezeichnen die Längen der entsprechenden Array-Dimensionen, d.h. im zweidimensionalen Fall den Zeilen und Spalten. In anderen Worten: Die Gestalt oder Shape eines Arrays ist ein Tupel mit der Anzahl der Elemente pro Achse (Dimension). In unserem Beispiel ist die Shape gleich (6, 3). Das bedeutet, das wir sechs Zeilen und drei Spalten haben.
x = np.array([ [67, 63, 87],
[77, 69, 59],
[85, 87, 99],
[79, 72, 71],
[63, 89, 93],
[68, 92, 78]])
print(np.shape(x))
Es gibt auch eine äquivalente Array-Property:
print(x.shape)
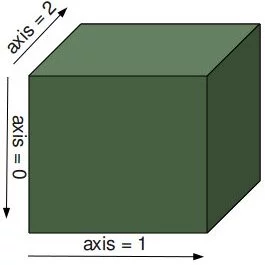
Die Shape eines Arrays sagt uns auch etwas über die Reihenfolge, in der die Indizes ausgeführt werden, d.h. zuerst die Zeilen, dann die Spalten und dann gegebenenfalls eine weitere Dimension oder weitere Dimensionen.
shape kann auch dazu genutzt werden, die "Shape" eines Arrays zu ändern:
x.shape = (3, 6)
print(x)
x.shape = (2, 9)
print(x)
Viele haben sicherlich bereits vermutet, dass die neue Shape der Anzahl der Elemente des Arrays entsprechen muss, d.h. die totale Größe des neuen Arrays muss die gleiche wie die alte sein. Eine Ausnahme wird erhoben, wenn dies nicht der Fall ist, wenn man in unserem Fall zum Beispiel
x.shape = (4, 4)
eingibt.
Die Shape eines Skalars ist ein leeres Tupel:
x = np.array(11)
print(np.shape(x))
Im Folgenden sehen wir die Shape eines dreidimensionalen Arrays:
B = np.array([ [[111, 112], [121, 122]],
[[211, 212], [221, 222]],
[[311, 312], [321, 322]] ])
print(B.shape)
Indizierung und Teilbereichsoperator
Der Zugriff oder die Zuweisung an die Elemente eines Arrays funktioniert ähnlich wie bei den sequentiellen Datentypen von Python, d.h. den Listen und Tupeln. Außerdem haben wir verschiedene Möglichkeiten zu indizieren. Dies macht das Indizieren in NumPy sehr mächtig und ähnlich zum Indizieren und dem Teilbereichsoperator der Listen.
Einzelne Elemente zu indizieren funktioniert so, wie es die meisten wahrscheinlich erwarten:
F = np.array([1, 1, 2, 3, 5, 8, 13, 21])
# Ausgabe des ersten Elements von F
print(F[0])
# Ausgabe letztes Element von F
print(F[-1])
Mehrdimensionale Arrays indizieren:
A = np.array([ [3.4, 8.7, 9.9],
[1.1, -7.8, -0.7],
[4.1, 12.3, 4.8]])
print(A[1][0])
B = np.array([ [[111, 112], [121, 122]],
[[211, 212], [221, 222]],
[[311, 312], [321, 322]] ])
print(B[0][1][0])
Wir haben auf das Element in der zweiten Zeile, d.h. die Zeile mit dem Index 1, und der ersten Spalte (Index 0) zugegriffen. Auf dieses Element haben wir in der gleichen Art zugegriffen, wie wir mit einem Element in einer verschachtelten Python-Liste verfahren wären.
Es gibt aber auch eine Alternative: Wir benutzen nur ein Klammernpaar, und alle Indizes werden mit Kommas separiert:
print(A[1, 0])
Man muss sich aber der Tatsache bewusst sein, dass die zweite Art prinzipiell effizienter ist. Im ersten Fall erzeugen wir als Zwischenschritt ein Array A[1], in dem wir dann auf das Element mit dem Index 0 zugreifen. Dies entspricht in etwa dem Folgenden:
tmp = A[1]
print(tmp)
print(tmp[0])
Wir nehmen an, dass Sie bereits vertraut sind mit den
(slicing) von den Listen und Tupeln.
Das englische Verb "to slice" bedeutet in Deutsch "schneiden" oder auch "in Scheiben schneiden". Letztere Bedeutung entspricht auch der Arbeitsweise des Teilbereichsoperators in Python und NumPy. Man schneidet sich gewissermaßen eine "Scheibe" aus einem sequentiellen Datentyp oder einem Array heraus.
Die Syntax in NumPy ist analog zu der von Standardpython im Falle von eindimensionalen Arrays. Allerdings können wir "Slicing" auch auf mehrdimensionale Arrays anwenden.
Die allgemeine Syntax für den eindimensionalen Fall lautet wie folgt:
[start:stop:step]
Wir demonstrieren die Arbeitsweise des Teilbereichsoperators an einigen Beispielen. Wir beginnen mit dem einfachsten Fall, also dem eindimensionalen Array:
S = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
print(S[2:5])
print(S[:4])
print(S[6:])
print(S[:])
Die Anwendung des Teilbereichsoperators auf mehrdimensionale Arrays illustrieren wir in den folgenden Beispielen. Die Bereiche für jede Dimension werden durch Kommas getrennt:
A = np.array([
[11, 12, 13, 14, 15],
[21, 22, 23, 24, 25],
[31, 32, 33, 34, 35],
[41, 42, 43, 44, 45],
[51, 52, 53, 54, 55]])
print(A[:3, 2:])
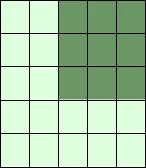
print(A[3:, :])

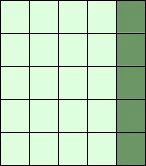
print(A[:, 4:])
Die folgenden beiden Beispiele benutzten auch noch den dritten Parameter step. Die reshape-Funktion benutzen wir, um ein eindimensionales Array in ein zweidimensionales zu wandeln. Wir werden reshape im folgenden Unterkapitel erklären:
X = np.arange(28).reshape(4, 7)
print(X)
print(X[::2, ::3])
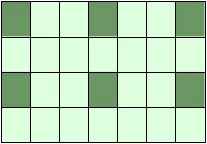
print(X[::, ::3])
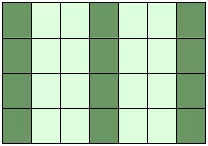

Falls die Zahl der Objekte in dem Auswahltupel kleiner als die Dimension N ist, dann wird ":" für die weiteren, nicht angegebenen Dimensionen angenommen:
A = np.array(
[ [ [45, 12, 4], [45, 13, 5], [46, 12, 6] ],
[ [46, 14, 4], [45, 14, 5], [46, 11, 5] ],
[ [47, 13, 2], [48, 15, 5], [52, 15, 1] ] ])
A[1:3, 0:2] # equivalent to A[1:3, 0:2, :]
Achtung: Während der Teilbereichsoperator bei Listen und Tupel neue Objekte erzeugt, generiert er bei NumPy nur eine Sicht (englisch: "view") auf das Originalarray. Dadurch erhalten wir eine andere Möglichkeit, das Array anzusprechen, oder besser einen Teil des Arrays. Daraus folgt, dass wenn wir etwas in einer Sicht verändern, wir auch das Originalarray verändern:
A = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
S = A[2:6]
S[0] = 22
S[1] = 23
print(A)
Wenn wir das analog bei Listen tun, sehen wir, dass wir eine Kopie erhalten. Genaugenommen müssten wir sagen, eine flache Kopie. Den Unterschied zwischen flacher und tiefer Kopie haben wir in unserem Kapitel "Flaches und tiefes Kopieren" ausführlich erklärt.
lst = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
lst2 = lst[2:6]
lst2[0] = 22
lst2[1] = 23
print(lst)
Will man prüfen, ob zwei Arrays auf den gleichen Speicherbereich zugreifen, so kann man die Funktion np.may_share_memory benutzen:
np.may_share_memory(A, B)
Um zu entscheiden, ob sich zwei Arrays A und B Speicher teilen, werden die Speichergrenzen von A und B berechnet. Die Funktion liefert True zurück, falls sie überlappen, und ansonsten False.
A = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
B = A[2:5]
np.may_share_memory(A, B)
Die Funktion kann allerdings falsch-positive Ergebnisse liefern, d.h. falls sie True zurückliefert, könnten die Arrays dennoch verschieden sein.
Im folgenden Beispiel haben B1 und B2 keine gemeinsamen Daten, aber die Speicherorte sind verzahnt, da beide ja "nur" eine View auf A darstellen:
A = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
B1 = A[::2]
B2 = A[1::2]
print(np.may_share_memory(B1, B2))
Das obige Beispiel ist ein falsch-positiv-Beispiel für may_share_memory in dem Sinn, dass jemand wegen der Ausgabe True denken könnte, dass die Arrays gemeinsamen Speicher hätten.
import numpy as np
X = np.array(
[[[3, 1, 2],
[4, 2, 2]],
[[-1, 0, 1],
[1, -1, -2]],
[[3, 2, 2],
[4, 4, 3]],
[[2, 2, 1],
[3, 1, 3]]])
print(X.shape)
Wir sehen, dass dieses Array eine Shape (4, 2, 3) hat. Wir benutzen nun die Slicing-Funktionalität, um uns die Schnitte durch die Dimensionen zu veranschaulichen:
print("Dimension 0 with size ", X.shape[0])
for i in range(X.shape[0]):
print(f"\nAusgabe von X[{i:1},:,:]:")
print(X[i,:,:])
print("\nDimension 1 with size ", X.shape[1])
for i in range(X.shape[1]):
print(f"\nAusgabe von X[:,{i:1},:]:")
print(X[:,i,:])
print("\nDimension 2 with size ", X.shape[2])
for i in range(X.shape[2]):
print(f"\nAusgabe von X[:,:,{i:1}]:")
print(X[:,:,i])
Arrays mit Nullen und Einsen
Arrays können auf zwei Arten mit Nullen und Einsen initialisiert werden. Die Methode ones(t) hat als Parameter ein Tupel t mit der Shape des Arrays und erzeugt entsprechend ein Array mit Einsen. Defaultmäßig wird es mit Float-Einsen gefüllt. Wenn man Integer-Einsen benötigt, kann man den optionalen Parameter dtype auf int setzen:
import numpy as np
E = np.ones((2, 3))
print(E)
F = np.ones((3, 4), dtype=int)
print(F)
Was wir über die Methode ones gesagt haben, gilt analog auch für die Methode zeros, wie wir im folgenden Beispiel erkennen können:
Z = np.zeros((2, 4))
print(Z)
Z = np.zeros((2, 4), dtype=int)
print(Z)
Es gibt noch eine andere interessante Möglichkeit, ein Array mit Einsen oder Nullen zu erzeugen, wenn es die gleiche Shape wie ein anderes existierendes Array 'a' haben soll. Für diesen Zweck stellt NumPy die Methoden ones_like und zeros_like zur Verfügung:
x = np.array([2, 5, 18, 14, 4])
E = np.ones_like(x)
print(E)
Z = np.zeros_like(x)
print(Z)
Arrays kopieren
numpy.copy(A) und A.copy()
Zum Kopieren eines NumPy-Arrays A gibt es generell zwei Möglichkeiten:
numpy.copy(A)A.copy()
Beide sind nahezu gleich und liefern jeweils eine Kopie des Arrays A zurück.
Sie unterscheiden sich aber beim Defaultwert des optionalen Parameters. Bei numpy.copy(obj) steht der Defaultwert auf order='K', und bei obj.copy() steht er auf order='C'.
| Parameter | Bedeutung |
|---|---|
| obj | array-ähnliche Eingabedaten |
| order | Die möglichen Werte sind {'C', 'F', 'A', 'K'}. Dieser Parameter kontrolliert das Speicher-Layout der Kopie. 'C' bedeutet C-Reihenfolge oder C-zusammenhängend, 'F' Fortran-zusammenhängend, 'A' verhält sich wie 'F', falls das Objekt 'obj' in Fortran-Reihenfolge ist, ansonsten verhält sich 'A' wie 'C'. 'K' bedeutet, dass das Layout von 'obj' so nahe wie möglich realisiert werden soll. |
Zusammenhängend gespeicherte Arrays
Um den Parameter order zu verstehen, gehen wir noch kurz auf den Begriff "zusammenhängend" (englisch "contiguous") ein. Die Speicherstruktur eines Arrays wird als zusammenhängend bezeichnet, wenn die Speicherung eines Arrays entweder C-zusammenhängend (C_CONTIGUOUS) oder Fortran-zusammenhängend (F_CONTIGUOUS) erfolgt. Betrachten wir dazu folgendes Array:
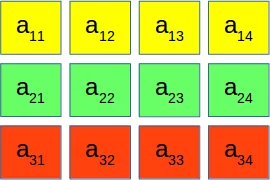
Wenn dieses Array zeilenweise abgespeichert ist, spricht man von C-zusammenhängend. Wir veranschaulichen dies im folgenden Bild:

Wird ein Array entsprechend spaltenweise abgespeichert, so bezeichnet man dies als F-zusammenhängend:

Wir demonstrieren nun, wie man die Speicherart mittels des Parameters order bestimmen kann:
import numpy as np
F = np.array([[11, 12, 13, 14],
[21, 22, 23, 24],
[31, 32, 33, 34]], order='F')
C = F.copy()
C2 = np.copy(F)
print("F array: \n", F)
print("C array: \n", C)
print("Ist F 'C continuous?': ", F.flags['C_CONTIGUOUS'])
print("Ist C 'C continuous?': ", C.flags['C_CONTIGUOUS'])
print("Ist C 'C continuous?': ", C2.flags['C_CONTIGUOUS'])
Transponiert man ein Array, werden die Daten nicht umgespeichert, sondern lediglich das strides-Attribut entsprechend angepasst, d.h. die Speicherung wird anders interpretiert.
T = C.transpose()
print(C.flags['C_CONTIGUOUS'])
print(T.flags['C_CONTIGUOUS'])
print(T.strides, C.strides)
T = F.transpose()
print(F.flags['C_CONTIGUOUS'])
print(T.flags['C_CONTIGUOUS'])
print(T.strides, F.strides)
Wir sehen, dass F.strides das Tupel (8, 24) zurückliefert. Dies besagt, dass man 24 Bytes -- was drei Zahlen à 8 Bytes entspricht -- überspringen muss, um von einem Arrayelement zum benachbarten Spaltenelement zu kommen. In anderen Worten: Wegen der Fortran-zusammenhängenden Speicherung liegen im Speicher zwischen den Werten von F[1, 1] und F[1, 2] die Werte von F[2, 1] und F[3, 1]. Die erste Komponente F.strides besagt, dass man entsprechend 8 Bytes überspringen muss, um zum benachbarten Element der nächsten Zeile zu kommen. Also zwischen den Werten von F[1, 1] und F[2, 1] liegen keine weiteren Werte.
Im Folgenden können wir noch sehen, wie sich die verschiedenen möglichen Werte für order auswirken.
order_values = ['C', 'F', 'A', 'K']
for order in order_values:
R1 = F.copy(order=order)
R2 = C.copy(order=order)
print(f"R1: order='{order}': ",
R1.flags['C_CONTIGUOUS'],
R1.flags['F_CONTIGUOUS'])
print(f"R2: order='{order}': ",
R2.flags['C_CONTIGUOUS'],
R2.flags['F_CONTIGUOUS'])
Identitäts-Array
In der linearen Algebra versteht man unter der Identitätsmatrix oder Einheitsmatrix eine quadratische Matrix, deren Hauptdiagonalelemente eins und deren Außerdiagonalelemente null sind.
NumPy bietet zwei Möglichkeiten, solche Arrays zu erzeugen:
- identy
- eye
Die identity-Funktion
Wir können Identitäts-Arrays mit der Funktion identity generieren:
identity(n, dtype=None)
| Parameter | Bedeutung |
|---|---|
| n | Eine Integer-Zahl, welche die Anzahl der Zeilen und Spalten der Ausgabe definiert, d.h. 'n' x 'n' |
| dtype | Ein optionales Argument, welches den Datentyp des Ergebnisses definiert. Der Default ist 'float' |
Die Ausgabe von identity ist ein n x n-Array, in dem die Elemente auf der Hauptdiagonalen auf 1 gesetzt sind und alle anderen Elemente auf 0.
import numpy as np
print(np.identity(4))
print(np.identity(4, dtype=int))
Die eye-Funktion
Die Funktion eye bietet eine andere Möglichkeit, Identitätsarrays, aber auch allgemeine Diagonalarrays, mit Einsen zu erzeugen. Die Ausgabe von eye ist ein zweidimensionales Array, in dem die Elemente auf der Hauptdiagonalen auf 1 gesetzt sind und alle anderen Elemente auf 0.
eye(N, M=None, k=0, dtype=float)
| Parameter | Bedeutung |
|---|---|
| N | Eine Integer-Zahl, welche die Anzahl der Zeilen des Ausgebearrays bestimmt. |
| M | Eine Integer-Zahl, welche die Spalten des Ausgabearrays bestimmt. Falls dieser Parameter nicht gesetzt ist oder None ist, wird er per Default auf 'N' gesetzt. |
| k | Mit 'k' wird die Position der Diagonalen gesetzt. Der Default ist 0. 0 bezeichnet die Hauptdiagonale. Ein positiver Wert bezeichnet eine obere Diagonale und ein negativer Wert eine untere Diagonale. |
| dtype | Ein optionales Argument, welches den Datentyp des Ergebnisses definiert. Der Default ist 'float'. |
eye liefert ein ndarray der Shape (N, M) zurück. Alle Elemente dieses Arrays sind 0 außer denen auf der k-ten Diagonale, die auf 1 gesetzt sind.
import numpy as np
print(np.eye(5, 8, k=1, dtype=int))
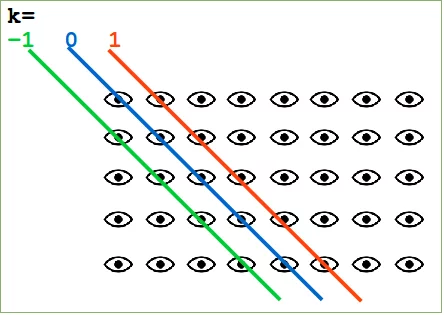
Die Arbeitsweise des Parameters d von eye illustrieren wir in folgendem Diagramm:

 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen

