Magische Methoden und Operatorüberladung
Einführung

Die sogenannten magischen Methoden haben nichts mit Zauberei zu tun. Sie haben sie bereits in den vorherigen Kapiteln unseres Tutorials gesehen. Sie sind spezielle Methoden mit festen Namen. Sie sind die Methoden mit dieser ungeschickten Syntax, d. H. Die doppelten Unterstriche am Anfang und am Ende. Sie sind auch schwer zu besprechen. Wie spricht man einen Methodennamen wie __init__ aus oder sagt er aus? "Unterstrich Unterstrich Init Unterstrich Unterstrich" klingt schrecklich und ist fast ein Zungenbrecher. "Double Underscore Init Double Underscore" ist viel besser, aber der ideale Weg ist "Dunder Init Dunder" Deshalb werden magische Methoden Methoden manchmal als Dunder Methoden bezeichnet !
Was ist also Magie an der __init__ Methode? Die Antwort lautet: Sie müssen es nicht direkt aufrufen. Der Aufruf erfolgt hinter den Kulissen. Wenn Sie eine Instanz x einer Klasse A mit der Anweisung "x = A ()" erstellen, führt Python die erforderlichen Aufrufe für __new__ und __init__ aus.
Gegen Ende dieses Kapitels unseres Tutorials werden wir die Methode __call__ einführen. Es wird von vielen Anfängern und sogar fortgeschrittenen Programmierern von Python übersehen. Es ist eine Funktionalität, die viele Programmiersprachen nicht haben, daher suchen Programmierer im Allgemeinen nicht danach. Mit der Methode __call__ können Python-Programmierer Klassen schreiben, in denen sich die Instanzen wie Funktionen verhalten. Beide Funktionen und die Instanzen solcher Klassen werden als aufrufbare Dateien bezeichnet.
Im Verlauf dieses Tutorials sind wir häufig auf das Konzept der Überlastung von Bedienern gestoßen. Wir hatten das Pluszeichen verwendet, um numerische Werte hinzuzufügen, Zeichenfolgen zu verketten oder Listen zu kombinieren:
4 + 5
3.8 + 9
"Peter" + " " + "Pan"
[3,6,8] + [7,11,13]

Es ist sogar möglich, den Operator "+" sowie alle anderen Operatoren für die Zwecke Ihrer eigenen Klasse zu überladen. Dazu müssen Sie den zugrunde liegenden Mechanismus verstehen. Für jedes Bedienerzeichen gibt es eine spezielle (oder "magische") Methode. Die magische Methode für das "+" - Zeichen ist die __add__ Methode. Für "-" ist es __sub__ und so weiter. Wir haben eine vollständige Liste aller magischen Methoden etwas weiter unten.
Der Mechanismus funktioniert folgendermaßen: Wenn wir einen Ausdruck "x + y" haben und x eine Instanz der Klasse K ist, überprüft Python die Klassendefinition von K. Wenn K eine Methode __add__ hat, ist dies der Fall aufgerufen mit x .__ add __ (y), sonst erhalten wir eine Fehlermeldung:
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unsupported operand type(s) for +: 'K' and 'K'
Überblick über magische Methoden
Binäroperatoren
| Operator | Methode |
|---|---|
| + | object.__add__(self, other) |
| - | object.__sub__(self, other) |
| * | object.__mul__(self, other) |
| // | object.__floordiv__(self, other) |
| / | object.__truediv__(self, other) |
| % | object.__mod__(self, other) |
| ** | object.__pow__(self, other[, modulo]) |
| << | object.__lshift__(self, other) |
| >> | object.__rshift__(self, other) |
| & | object.__and__(self, other) |
| ^ | object.__xor__(self, other) |
| | | object.__or__(self, other) |
Erweiterte Zuweisungen
| Operator | Methode |
|---|---|
| += | object.__iadd__(self, other) |
| -= | object.__isub__(self, other) |
| *= | object.__imul__(self, other) |
| /= | object.__idiv__(self, other) |
| //= | object.__ifloordiv__(self, other) |
| %= | object.__imod__(self, other) |
| **= | object.__ipow__(self, other[, modulo]) |
| <<= | object.__ilshift__(self, other) |
| >>= | object.__irshift__(self, other) |
| &= | object.__iand__(self, other) |
| ^= | object.__ixor__(self, other) |
| |= | object.__ior__(self, other) |
Unäre Operatoren
| Operator | Methode |
|---|---|
| - | object.__neg__(self) |
| + | object.__pos__(self) |
| abs() | object.__abs__(self) |
| ~ | object.__invert__(self) |
| complex() | object.__complex__(self) |
| int() | object.__int__(self) |
| long() | object.__long__(self) |
| float() | object.__float__(self) |
| oct() | object.__oct__(self) |
| hex() | object.__hex__(self |
Vergleichsoperatoren
| Operator | Methode |
|---|---|
| < | object.__lt__(self, other) |
| <= | object.__le__(self, other) |
| == | object.__eq__(self, other) |
| != | object.__ne__(self, other) |
| >= | object.__ge__(self, other) |
| > | object.__gt__(self, other) |
Beispielklasse: Länge
Wir zeigen die Längenklasse und wie Sie den Operator "+" für Ihre eigene Klasse überladen können. Dazu müssen wir die Methode __add__ überladen. Unsere Klasse enthält auch die Methoden __str__ und __repr__. Die Instanzen der Klasse Länge enthalten Längen- oder Entfernungsinformationen. Die Attribute einer Instanz sind self.value und self.unit.
Diese Klasse ermöglicht es uns, Ausdrücke mit gemischten Einheiten wie dieser zu berechnen:
2,56 m + 3 yd + 7,0 in + 7,03 cm </ pre> Die Klasse kann folgendermaßen verwendet werden:
from unit_conversions import Length
L = Length
print(L(2.56,"m") + L(3,"yd") + L(7.8,"in") + L(7.03,"cm"))
Die Auflistung der Klasse:
class Length: #Länge
__metric = {"mm" : 0.001, "cm" : 0.01, "m" : 1, "km" : 1000,
"in" : 0.0254, "ft" : 0.3048, "yd" : 0.9144,
"mi" : 1609.344 }
def __init__(self, value, unit = "m" ):
self.value = value
self.unit = unit
def Convert2Metres(self): # in Meter umrechnen
return self.value * Length.__metric[self.unit]
def __add__(self, other):
l = self.Convert2Metres() + other.Convert2Metres()
return Length(l / Length.__metric[self.unit], self.unit )
def __str__(self):
return str(self.Convert2Metres())
def __repr__(self):
return "Length(" + str(self.value) + ", '" + self.unit + "')"
x = Length(4)
print(x)
y = eval(repr(x))
z = Length(4.5, "yd") + Length(1)
print(repr(z))
print(z)
x = Length(4)
print(x)
y = eval(repr(x))
z = Length(1, "ft") + Length(1)
print(repr(z))
print(z)
4.280839 * 0.3048
Wir verwenden die Methode __iadd__, um die erweiterte Zuweisung zu implementieren:
def __iadd__(self, other):
l = self.Convert2Metres() + other.Convert2Metres()
self.value = l / Length.__metric[self.unit]
return self
Jetzt können wir folgende Aufgaben schreiben:
x += Length(1)
x += Length(4, "yd")
Wir haben im obigen Beispiel 1 Meter hinzugefügt, indem wir "x + = Länge (1))" geschrieben haben. Mit Sicherheit werden Sie uns zustimmen, dass es bequemer wäre, stattdessen einfach "x + = 1" zu schreiben. Wir möchten auch Ausdrücke wie "Länge (5," yd ") + 4,8" ähnlich behandeln. Wenn also jemand einen Typ int oder float verwendet, nimmt unsere Klasse ihn automatisch für "meter" und konvertiert ihn in ein Length-Objekt. Es ist einfach, unsere __add__ und __iadd__ Methode für diese Aufgabe anzupassen. Wir müssen lediglich den Typ des Parameters "other" überprüfen:
def __add__(self, other):
if type(other) == int or type(other) == float:
l = self.Convert2Metres() + other
else:
l = self.Convert2Metres() + other.Convert2Metres()
return Length(l / Length.__metric[self.unit], self.unit )
def __iadd__(self, other):
if type(other) == int or type(other) == float:
l = self.Convert2Metres() + other
else:
l = self.Convert2Metres() + other.Convert2Metres()
self.value = l / Length.__metric[self.unit]
return self
Es ist eine sichere Wette, dass jemand, der für eine Weile mit dem Hinzufügen von ganzen Zahlen arbeitet und von der rechten Seite schwebt, dasselbe von der linken Seite haben möchte! Was passiert, wenn wir die folgende Codezeile ausführen:
x = 5 + Länge (3," yd ")
Wir werden eine Ausnahme bekommen:
AttributeError: 'int' object has no attribute 'Converse2Metres'
Natürlich muss die linke Seite vom Typ "Length" sein, da Python sonst versucht, die Methode __add__ von int anzuwenden, die Length-Objekte nicht als zweites Argument verarbeiten kann!
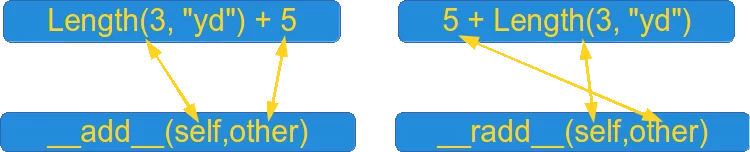
Python bietet auch eine Lösung für dieses Problem. Es ist die __radd__ Methode. Das funktioniert so: Python versucht, den Ausdruck "5 + Länge (3, 'yd')" auszuwerten. Zuerst wird int.__add__ (5, Länge (3, 'yd')) aufgerufen, wodurch eine Ausnahme ausgelöst wird. Danach wird versucht, Length.__radd__ (Length (3, "yd"), 5) aufzurufen. Es ist leicht zu erkennen, dass die Implementierung von __radd__ analog zu __add__ ist:
def __radd__(self, other):
if type(other) == int or type(other) == float:
l = self.Convert
l = self.Convert2Metres() + other.Convert2Metres()
return Length(l / Length.__metric[self.unit], self.unit )
Es ist empfohlen, die Methode __add__ in der Methode __radd__ zu verwenden:
def __radd__(self, other):
return Length.__add__(self,other)
Das folgende Diagramm zeigt die Beziehung zwischen __add__ und __radd__:
Die call Methode
Bevor wir zur Methode __call__ kommen, müssen wir wissen, was ein Callable ist. Im Allgemeinen ist ein "aufrufbar" ein Objekt, das wie eine Funktion aufgerufen werden kann und sich wie eine verhält. Alle Funktionen sind auch aufrufbar. Python bietet eine Funktion mit dem Namen callable. Mit Hilfe dieser Funktion können wir feststellen, ob ein Objekt aufrufbar ist oder nicht.
Die Funktion callable gibt einen booleschen Wahrheitswert zurück, der angibt, ob das als Argument übergebene Objekt wie eine Funktion aufgerufen werden kann oder nicht. Zusätzlich zu den Funktionen haben wir bereits eine andere Form von callables gesehen: Klassen
def der_antwort(question):
return 42
print("der_antwort: ", callable(der_antwort))
Die Methode __call__ kann verwendet werden, um die Instanzen der Klasse in aufrufbare Dateien umzuwandeln. Funktionen sind aufrufbare Objekte. Ein aufrufbares Objekt ist ein Objekt, das verwendet werden kann und sich wie eine Funktion verhält, aber möglicherweise keine Funktion ist. Mit der Methode __call__ können Klassen so definiert werden, dass die Instanzen aufrufbare Objekte sind. Die __call__ Methode wird aufgerufen, wenn die Instanz" wie eine Funktion "aufgerufen wird, d. H. Unter Verwendung von Klammern. Die folgende Klassendefinition ist die einfachste Möglichkeit, eine Klasse mit einer __call__ Methode zu definieren.
class Essen:
def __call__(self):
return "spam"
foo = Essen()
bar = Essen()
print(foo(), bar())
Das vorherige Klassenbeispiel ist extrem einfach, aber praktisch unbrauchbar. Immer wenn wir eine Instanz der Klasse erstellen, erhalten wir eine aufrufbare. Diese Callables definieren immer dieselbe konstante Funktion. Eine Funktion ohne Eingabe und konstante Ausgabe "Spam". Wir werden nun eine Klasse definieren, die etwas nützlicher ist. Wir definieren eine Klasse mit dem Namen TriangleArea. Diese Klasse hat nur eine Methode, nämlich die Methode __call__. Die Methode __call__ berechnet die Fläche eines beliebigen Dreiecks, wenn die Länge der drei Seiten angegeben ist.
class DreieckFläche:
def __call__(self, a, b, c):
p = (a + b + c) / 2
result = (p * (p - a) * (p - b) * (p - c)) ** 0.5
return result
fläche = DreieckFläche()
print(fläche(3, 4, 5))
Dieses Programm gibt 6.0 zurück. Diese Klasse ist nicht sehr aufregend, obwohl wir eine beliebige Anzahl von Instanzen erstellen können, in denen jede Instanz nur eine unveränderte __call__ -Funktion der TrianlgeClass ausführt. Wir können keine Parameter an die Instanziierung übergeben und der __call__ jeder Instanz gibt den Wert der Fläche des Dreiecks zurück. Jede Instanz verhält sich also wie die Bereichsfunktion.
Nach den beiden sehr didaktischen und nicht sehr praktischen Beispielen möchten wir im Folgenden ein praktischeres Beispiel demonstrieren. Wir definieren eine Klasse, mit der lineare Gleichungen definiert werden können:
class GeradeLinien():
def __init__(self, m, c):
self.slope = m
self.y_intercept = c
def __call__(self, x):
return self.slope * x + self.y_intercept
linie = GeradeLinien(0.4, 3)
for x in range(-5, 6):
print(x, linie(x))
Wir werden diese Klasse jetzt verwenden, um einige gerade Linien zu erstellen und sie mit matplotlib zu visualisieren:
linien = []
linien.append(GeradeLinien(1, 0))
linien.append(GeradeLinien(0.5, 3))
linien.append(GeradeLinien(-1.4, 1.6))
import matplotlib.pyplot as plt
import numpy as np
X = np.linspace(-5,5,100)
for index, linie in enumerate(linien):
line = np.vectorize(linie)
plt.plot(X, line(X), label='Linie' + str(index))
plt.title('Gerade Linien')
plt.xlabel('x', color='#1C2833')
plt.ylabel('y', color='#1C2833')
plt.legend(loc='upper left')
plt.grid()
plt.show()
Spannend ist auch unser nächstes Beispiel. Die Klasse FuzzyDreieckFläche definiert eine __call__ Methode, die ein Fuzzy-Verhalten in die Berechnungen der Fläche implementiert. Das Ergebnis sollte mit einer Wahrscheinlichkeit von p korrekt sein, z. 0,8. Wenn das Ergebnis nicht korrekt ist, liegt das Ergebnis in einem Bereich von ± v%. z.B. 0,1.
import random
class FuzzyDreieckFläche:
def __init__(self, p=0.8, v=0.1):
self.p, self.v = p, v
def __call__(self, a, b, c):
p = (a + b + c) / 2
result = (p * (p - a) * (p - b) * (p - c)) ** 0.5
if random.random() <= self.p:
return result
else:
return random.uniform(result-self.v,
result+self.v)
fläche1 = FuzzyDreieckFläche()
fläche2 = FuzzyDreieckFläche(0.5, 0.2)
for i in range(12):
print(f"{fläche1(3, 4, 5):4.3f}, {fläche2(3, 4, 5):4.2f}")
Beachten Sie, dass diese Ausgabe bei jedem Anruf unterschiedlich ist! Wir können sehen, dass wir in den meisten Fällen den richtigen Wert für das Gebiet erhalten, aber manchmal nicht.
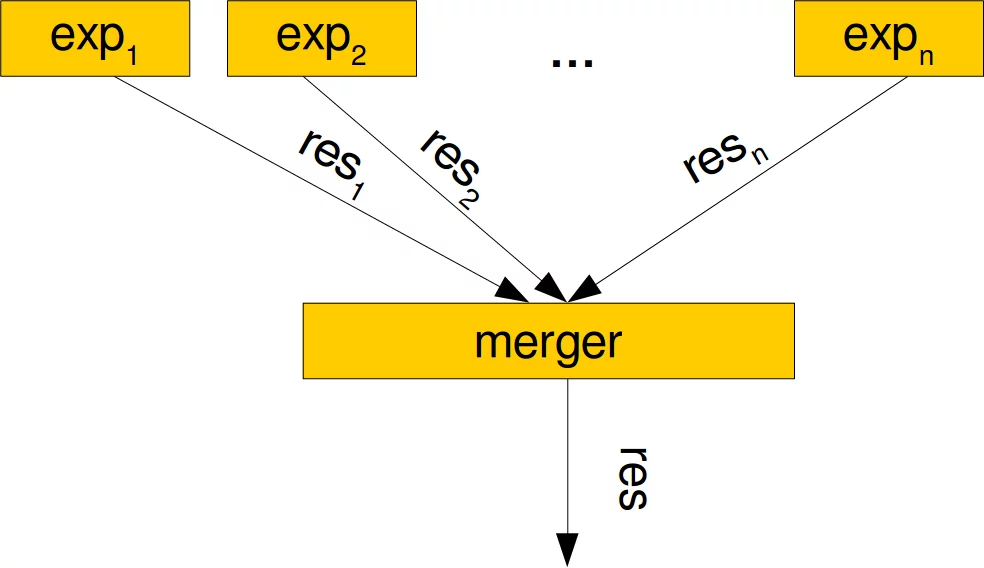
Wir können viele verschiedene Instanzen der vorherigen Klasse erstellen. Jede dieser Funktionen verhält sich wie eine Bereichsfunktion, die abhängig von den Instanziierungsparametern p und v einen Wert für den Bereich zurückgibt, der möglicherweise korrekt ist oder nicht. Wir können diese Instanzen als Experten (Expertenfunktionen) betrachten, die in den meisten Fällen zurückgegeben werden die richtige Antwort, wenn wir p-Werte nahe 1 verwenden. Wenn der Wert v nahe Null ist, ist der Fehler, wenn überhaupt, klein. Die nächste Aufgabe wäre das Zusammenführen solcher Experten. Nennen wir sie exp1, exp2, ..., expn, um ein verbessertes Ergebnis zu erzielen. Wir können über die Ergebnisse abstimmen, d. H. Wir geben den am häufigsten vorkommenden Wert, den richtigen Wert, zurück. Alternativ können wir das arithmetische Mittel berechnen. Wir werden beide Möglichkeiten in unserer Klasse FuzzyTriangleArea implementieren:
from random import uniform, random
from collections import Counter
class FuzzyDreieckFläche:
def __init__(self, p=0.8, v=0.1):
self.p, self.v = p, v
def __call__(self, a, b, c):
p = (a + b + c) / 2
result = (p * (p - a) * (p - b) * (p - c)) ** 0.5
if random() <= self.p:
return result
else:
return uniform(result-self.v,
result+self.v)
class MergeExperts:
def __init__(self, mode, *experts):
self.mode, self.experts = mode, experts
def __call__(self, a, b, c):
results= [exp(a, b, c) for exp in self.experts]
if self.mode == "Stimme":
c = Counter(results)
return c.most_common(1)[0][0]
elif self.mode == "Mittelwert":
return sum(results) / len(results)
rvalues = [(uniform(0.7, 0.9), uniform(0.05, 0.2)) for _ in range(20)]
experts = [FuzzyDreieckFläche(p, v) for p, v in rvalues]
merger1 = MergeExperts("Stimme", *experts)
print(merger1(3, 4, 5))
merger2 = MergeExperts("Mittelwert", *experts)
print(merger2(3, 4, 5))
Das folgende Beispiel definiert eine Klasse, mit der wir willkürliche Polynomfunktionen erstellen können:
class Polynomial:
def __init__(self, *coefficients):
self.coefficients = coefficients[::-1]
def __call__(self, x):
res = 0
for index, coeff in enumerate(self.coefficients):
res += coeff * x** index
return res
# eine konstante Funktion
p1 = Polynomial(42)
# eine gerade Linie
p2 = Polynomial(0.75, 2)
# ein Polynom dritten Grades
p3 = Polynomial(1, -0.5, 0.75, 2)
for i in range(1, 10):
print(i, p1(i), p2(i), p3(i))
Weitere interessante Beispiele für die Funktion __call__ finden Sie in unserem Tutorial in den Kapiteln Decorators und Memoization with Decorators. Sie können auch unser Kapitel über Polynome lesen.
class Plist(list):
def __init__(self, l):
list.__init__(self, l)
def push(self, item):
self.append(item)
if __name__ == "__main__":
x = Plist([3,4])
x.push(47)
print(x)
Dies bedeutet, dass alle zuvor eingeführten binären und erweiterten Zuweisungsoperatoren auch in der "umgekehrten" Version vorhanden sind:
__radd__, __rsub__, __rmul__ usw.
Übungen
Übung 1
Schreiben Sie eine Klasse mit dem Namen Ccy, ähnlich der zuvor definierten Längenklasse. Ccy sollte Werte in verschiedenen Währungen enthalten, z. "EUR", "GBP" oder "USD". Eine Instanz sollte den Betrag und die Währungseinheit enthalten. Die Klasse, die Sie als Übung entwerfen möchten, lässt sich am besten anhand der folgenden Beispielsitzung beschreiben:
from currencies import Ccy
v1 = Ccy(23.43, "EUR")
v2 = Ccy(19.97, "USD")
print(v1 + v2)
print(v2 + v1)
print(v1 + 3) # an int or a float is considered to be a EUR value
print(3 + v1)%%writefile currencies.py
"""
Mit der Klasse "Ccy" können Geldwerte in verschiedenen Währungen definiert werden. Eine Ccy-Instanz hat die Zeichenfolgenattribute 'Einheit' (z. B. 'CHF', 'CAD' oder 'EUR' und den 'Wert' als Float.
Ein Währungsobjekt besteht aus einem Wert und der entsprechenden Einheit.
"""
class Ccy:
währungen = {'CHF': 1.0821202355817312,
'CAD': 1.488609845538393,
'GBP': 0.8916546282920325,
'JPY': 114.38826536281809,
'EUR': 1.0,
'USD': 1.11123458162018}
def __init__(self, value, unit="EUR"):
self.value = value
self.unit = unit
def __str__(self):
return "{0:5.2f}".format(self.value) + " " + self.unit
def changeTo(self, new_unit):
"""
An Ccy object is transformed from the unit "self.unit" to "new_unit"
"""
self.value = (self.value / Ccy.währungen[self.unit] * Ccy.währungen[new_unit])
self.unit = new_unit
def __add__(self, other):
"""
Definiert den Operator '+'.
Wenn other ein CCy-Objekt ist, werden die Währungswerte angegeben
werden hinzugefügt und das Ergebnis ist die Einheit von
selbst. Wenn other ein int oder ein float ist, wird other will
als Euro-Wert behandelt werden.
"""
if type(other) == int or type(other) == float:
x = (other * Ccy.währungen[self.unit])
else:
x = (other.value / Ccy.währungen[other.unit] * Ccy.währungen[self.unit])
return Ccy(x + self.value, self.unit)
def __iadd__(self, other):
"""
Ähnlich wie __add__
"""
if type(other) == int or type(other) == float:
x = (other * Ccy.währungen[self.unit])
else:
x = (other.value / Ccy.währungen[other.unit] * Ccy.währungen[self.unit])
self.value += x
return self
def __radd__(self, other):
res = self + other
if self.unit != "EUR":
res.changeTo("EUR")
return res
#__sub__, __isub__ und __rsub__ können analog definiert werden
from currencies import Ccy
x = Ccy(10,"USD")
y = Ccy(11)
z = Ccy(12.34, "JPY")
z = 7.8 + x + y + 255 + z
print(z)
lst = [Ccy(10,"USD"), Ccy(11), Ccy(12.34, "JPY"), Ccy(12.34, "CAD")]
z = sum(lst)
print(z)
Ein weiterer interessanter Aspekt dieser Währungsumrechnerklasse in Python kann gezeigt werden, wenn wir die Multiplikation hinzufügen. Sie werden leicht verstehen, dass es keinen Sinn macht, Ausdrücke wie " 12.4 € * 3.4 USD " (oder in Präfixnotation: "€ 12.4 $ 3.4") zuzulassen, aber es ist absolut sinnvoll, "3" zu bewerten 4,54 € ". Sie finden die neue Währungsumrechnerklasse mit den neu hinzugefügten Methoden für __mul__,__imul__ und __rmul__ in der folgenden Liste:
%%writefile currency_converter.py
"""
Mit der Klasse "Ccy" können Geldwerte in verschiedenen Währungen definiert werden. Eine Ccy-Instanz hat die Zeichenfolgenattribute 'Einheit' (z. B. 'CHF', 'CAD' oder 'EUR' und den 'Wert' als Float.
Ein Währungsobjekt besteht aus einem Wert und der entsprechenden Einheit.
"""
class Ccy:
währungen = {'CHF': 1.0821202355817312,
'CAD': 1.488609845538393,
'GBP': 0.8916546282920325,
'JPY': 114.38826536281809,
'EUR': 1.0,
'USD': 1.11123458162018}
def __init__(self, value, unit="EUR"):
self.value = value
self.unit = unit
def __str__(self):
return "{0:5.2f}".format(self.value) + " " + self.unit
def __repr__(self):
return 'Ccy(' + str(self.value) + ', "' + self.unit + '")'
def changeTo(self, new_unit):
"""
Ein Ccy-Objekt wird von der Einheit "self.unit" in "new_unit" umgewandelt.
"""
self.value = (self.value / Ccy.währungen[self.unit] * Ccy.währungen[new_unit])
self.unit = new_unit
def __add__(self, other):
"""
Definiert den Operator '+'.
Wenn other ein CCy-Objekt ist, werden die Währungswerte angegeben
werden hinzugefügt und das Ergebnis ist die Einheit von
selbst. Wenn other ein int oder ein float ist, wird other will
als Euro-Wert behandelt werden.
"""
if type(other) == int or type(other) == float:
x = (other * Ccy.währungen[self.unit])
else:
x = (other.value / Ccy.währungen[other.unit] * Ccy.währungen[self.unit])
return Ccy(x + self.value, self.unit)
def __iadd__(self, other):
"""
Ähnlich wie __add__
"""
if type(other) == int or type(other) == float:
x = (other * Ccy.währungen[self.unit])
else:
x = (other.value / Ccy.währungen[other.unit] * Ccy.währungen[self.unit])
self.value += x
return self
def __radd__(self, other):
res = self + other
if self.unit != "EUR":
res.changeTo("EUR")
return res
# __sub__, __isub__ und __rsub__ können analog definiert werden
def __mul__(self, other):
"""
Die Multiplikation wird nur als skalare Multiplikation definiert.
d.h. ein Geldwert kann mit einem int oder einem float multipliziert werden.
Es ist nicht möglich, sich mit Geldwerten zu multiplizieren
"""
if type(other)==int or type(other)==float:
return Ccy(self.value * other, self.unit)
else:
raise TypeError("unsupported operand type(s) for *: 'Ccy' and " + type(other).__name__)
def __rmul__(self, other):
return self.__mul__(other)
def __imul__(self, other):
if type(other)==int or type(other)==float:
self.value *= other
return self
else:
raise TypeError("unsupported operand type(s) for *: 'Ccy' and " + type(other).__name__)
Angenommen, Sie haben die Klasse unter dem Namen Currency_Converter gespeichert, können Sie sie in der Befehlsshell folgendermaßen verwenden:
from currency_converter import Ccy
x = Ccy(10.00, "EUR")
y = Ccy(10.00, "GBP")
x + y
print(x + y)
print(2*x + y*0.9)


 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen


