Python-Kurs

Neuronale Netzwerke

Einführung

Wenn wir von "Neuronalen Netzen" sprechen, meinen wir artifizielle neuronale Netze (ANN). Die Idee eines ANN basiert auf biologischen neuronalen Netzen, wie sie z.B. im Gehirn von Lebewesen vorkommen.

Die Basiseinheit eines neuronalen Netzes - sowohl eines artifiziellen als auch eines lebendigen - ist das Neuron. Ein biologisches Neuron besteht aus drei Hauptkomponenten: Dem Soma (Zellkörper), den Dendriten und dem Axon.

Die Dendriten zweigen aus dem Soma ab wie die Verzweigung eines Baumes und verjüngen sich mit jeder neuen Aufteilung. Sie erhalten Signale (Impulse) von anderen Neuronen an den Synapsen, wo sie sich mit anderen Zellen verbinden. Das Axon - wovon immer nur eines existiert - kommt ebenfalls aus dem Soma und erstreckt sich normalerweise über weitere Distanzen als die Dendriten. Es wird gebraucht, um das Ausgangssignal des Neurons an andere Neuronen zu übergeben oder genauer gesagt an die Synapsen anderer Neurone.

Biologisches Neuron

Die folgende Abbildung [Quasar Jarosz] (https://en.wikipedia.org/wiki/User:Quasar_Jarosz), aus Wikipedia, zeigt dies:

Abstraktion eines biologischen und eines artifiziellen Neurons

Auch wenn die obige Abbildung für eine/n Biologen/in schon eine Abstraktion darstellt, können wir sie noch mehr abstrahieren:

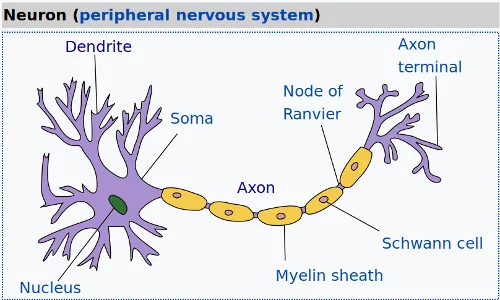
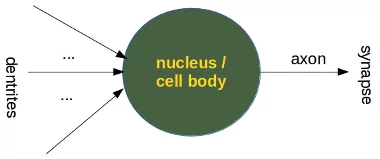
Ein Perceptron als Element eines artifiziellen neuronalen Netzwerks simuliert ein biologisches Neuron.

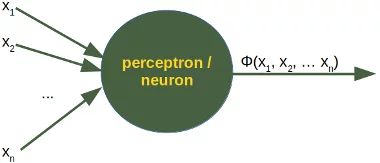
Was im Inneren eines solchen Perceptrons oder Neurons vorgeht, ist erstaunlich einfach. Die Eingangssignale werden mit den Gewichten (engl. "weights") multipliziert, jeder Eingang hat sein zugeordnetes Gewicht. So wird jeder Eingang individuell angepasst für jedes $x_i$. Wir können alle Eingänge als den Eingangsvektor verstehen und die zugehörigen Gewichte als den Gewichtsvektor.

Wenn also ein Signal ankommt, wird es mit dem Wert des Gewichts des individuellen Eingangs multipliziert, das diesem Eingang zugeordnet ist. So hat ein Neuron mit drei Eingängen auch drei Gewichte, die individuell angepasst werden können. Die Anpassung der Gewichte erfolgt normalerweise in der Lernphase des Netzes.

Danach werden die Eingangssignale summiert. Es ist auch möglich, einen sogenannten Bias "b" dazu zu addieren, der ein von anderen Neuronen unabhängiges Eingangssignal darstellt. Auch dieser Bias kann während der Lernphase angepasst werden.

Schliesslich wird er Ausgangswert festgelegt. Dafür wird eine Aktivierungs- oder Stufenfunktion Φ auf die gewichtete Summe der Eingangswerte angewendet.

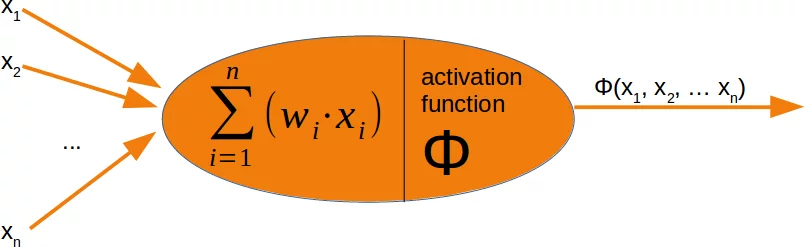
Die einfachste Form einer Aktivierungsfunktion ist eine Binärfunktion. Wenn das Ergebnis der Summation grösser als ein Schwellenwert s ist, ist das Ergebnis von $\Phi$ 1, sonst 0. $$ \Phi(x) = \left\{ \begin{array}{rl} 1 &\mbox{ wx + b > s} \\ 0 &\mbox{ otherwise} \end{array} \right. $$

Anzahl Neuronen in der Biologie

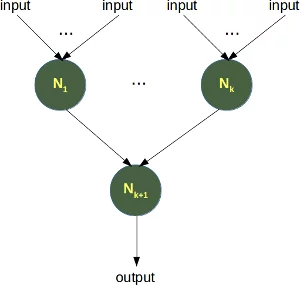
Wir werden im den folgenden Kapiteln artifizielle neuronale Netze verschiedener Grössen und Strukturen untersuchen. Interessant ist ein Blick auf die Gesamtzahl der Neuronen von verschiedenen Lebewesen.

Beim Fadenwurm Caenorhabditis elegans, einem der meist erforschten Modellorganismnen der modernen Biologie gibt es so genau 385 Neuronen. (Quelle Wikipedia).

Beim Menschen geht man bei aktuellen Schätzungen von etwa 86 Milliarden Nervenzellen aus.(Max Planck Institut für Hirnforschung Berlin).