Nächstes Kapitel: Nächste Nachbarn-Klassifikation mit sklearn
Nächste-Nachbarn-Klassifikation¶
Einführung¶
"Zeig mir deine Freunde und ich sag' dir wer du bist"
Das Konzept des Nächsten-Nachbarn-Klassifikators oder genauer es k-nächsten-Nachbarn-Klassifikators kann kaum einfacher beschrieben werden, wie mit diesem Sprichwort. Das ist eine alte Redensart, die es in vielen Sprachen und Kulturen gibt. Es wird auch in anderen Worten in der Bibel erwähnt: "Wer mit den Weisen umgeht, der wird weise; wer aber der Toren Geselle ist, der wird Unglück haben." (Sprüche 13,20)
Das k-Nearest-Neighbor Konzept ist also Teil unseres täglichen Lebens und unseres Urteilsvermögens: Stellen Sie sich vor Sie treffen eine Gruppe von Menschen. Sie sind alle jung, stylisch und sportlich. Sie reden über ihren Freund Ben, der gerade nicht dabei ist. Wie ist ihre Vorstellung zu Ben? Richtig, Sie werden wohl denken, dass Ben auch jung, stylisch und sportlich ist.
Wenn du erfährst dass Ben in einer Nachbarschaft lebt, in der konservativ gewählt wird und das Durchschnittseinkommen über 200.000 Dollar im Jahr liegt. Seine beiden direkten Nachbarn verdienen sogar mehr als 300.000 Dollar im Jahr. Was denkst du über Ben? Du wirst ihn sehr wahrscheinlich nicht für einen "Underdog" halten. Vielmehr wirst du glauben, dass er ebenfalls wohlhabend ist und höchst-wahrscheinlich nicht weniger als seine Nachbarn verdienen.
Betrachten wir das Konzept mehr aus der Richtung der Mathematik:
Wie im Kaptiel Aufteilungen der Daten dargelegt, benötigen wir gelabelte Lern- und Testdaten.
Im Unterschied zu anderen Klassifikatoren findet bei den reinen NächstenNachbarn-Klassifikatoren jedoch kein Lernen statt, sondern das sogenannte Lernset $LS$ ist Grundbestandteil des Klassifikators. Der k-Nächste_Nachbarn-Klassifikator (k-NN) arbeitet direkt mit den gelernten Stichproben, anstatt Regeln zu erstelln, wie dies andere Klassifizierungsmethoden tun.
Die Aufgabe der Klassifikation besteht in der Zuordnung von Kategorien oder Klassen zu einem Element einer zu klassifizierenden Mengen von Objekten.
Nächste-Nachbarn-Algorithmus:
Es ist eine Menge $K = \{c_1,c_2, \cdots, c_m\}$ von Kategorien gegeben, die auch Klassen genannt werden. z.B. {"male", "female"}.
Außerdem sei eine weitere Menge $LS$ gegeben, die gelabellte Objekte enthält.
$$LS = \{(o_1, c_{o_1}), (o_2, c_{o_2}), \cdots (o_n, c_{o_n}) \}$$
Da es keinen Sinn ergibt, dass man weniger gelabellte Objekte als Klassen hat, muss gelten:
$n > m$ und im allgemeinen sogar $n \ggg m$ (n sehr viel größer als m.)
Die Aufgabe der Klassifikation besteht nun darin einem Objekt $o$ ein Kategorie/Klasse $c$ zuzuordnen. Dazu müssen wir zwei Fälle unterscheiden:
- Fall:
Die Instanz $o$ ist in $LS$ enthalten, d.h. es gibt ein Tupel $(o, c) \in LS$
In diesem Fall nehmen wir die Klasse $c$ als Klassifikationsergebnis.
- Fall:
- Fall:
Nun nehmen wir an, dass $o$ nicht in $LS$ enthalten ist, genauer gesagt:
$\forall c \in C, (o, c) \not\in LS$
$o$ wird nun mit allen Instanzen von $LS$ verglichen. Eine Abstandsmetrik $d$ wird für die Vergleiche benutzt.
Wir bestimmen die $k$ nächsten Nachbarn von $o$, d.h. die Instanzen mit den kleinsten Entfernungen.
$k$ ist eine benutzerdefinierte positive ganze Zahl, die überlicherweise nicht sehr groß ist.
Um die $k$-nächsten Nachbarn zu bestimmen, ordnen wir $LS$ auf die foldende Art um:
$(o_{i_1}, c_{o_{i_1}}), (o_{i_2}, c_{o_{i_2}}), \cdots (o_{i_n}, c_{o_{i_n}})$
wobei für alle $1 \leq j \leq {n-1}$ gilt $d(o_{i_j}, o) \leq d(o_{i_{j+1}}, o)$ Die Menge der nächsten Nachbarn $N_k$ besteht aus den ersten $k$ Elementen dieser Ordnung, d.h.
$N_k = \{ (o_{i_1}, c_{o_{i_1}}), (o_{i_2}, c_{o_{i_2}}), \cdots (o_{i_k}, c_{o_{i_k}}) \}$
Die am häufigsten vorkommende Klasse in dieser Menge $N_k$ wird zum Ergebnis der Klassifikation $o$. Wenn es keine eindeutige Wenn sich keine KLasse eindeutig als häufigste bestimmen lässt, nehmen wir willkürlich eine der Kandidaten.
- Fall:
Es gibt keine allgemeine Möglichkeit, einen optimalen Wert für k zu definieren. Dieser Wert hängt von den Daten ab. In der Regel können wir sagen, dass bei zunehmendem k das Rauschen reduziert wird, andererseits werden die Grenzen jedoch weniger scharf.
Der Algorithmus für den k-Nearest-Neighbor Klassifikator ist einer der einfachsten von allen Machine Learning Algorithmen. k-NN gehört zu den Typen des instanzbasierten Lernens, oder lazy-Lernens. In der Theorie des Maschinellen Lernens wird Lazy-lernen als Lernmethode verstanden, in der die Verallgemeinerung der Trainingsdaten verzögert wird, bis eine Abfrage an das System vorgenommen wird. Andererseits haben wir das Eager-Lernen, wo das System die Trainingsdaten in der Regel verallgemeint, bevor es Abfragen erhält. In anderen Worten: Die Funktion wird nur lokal approximiert und alle Berechnungen werden bei der jeweils aktuellen Klassifikation durchgeführt.
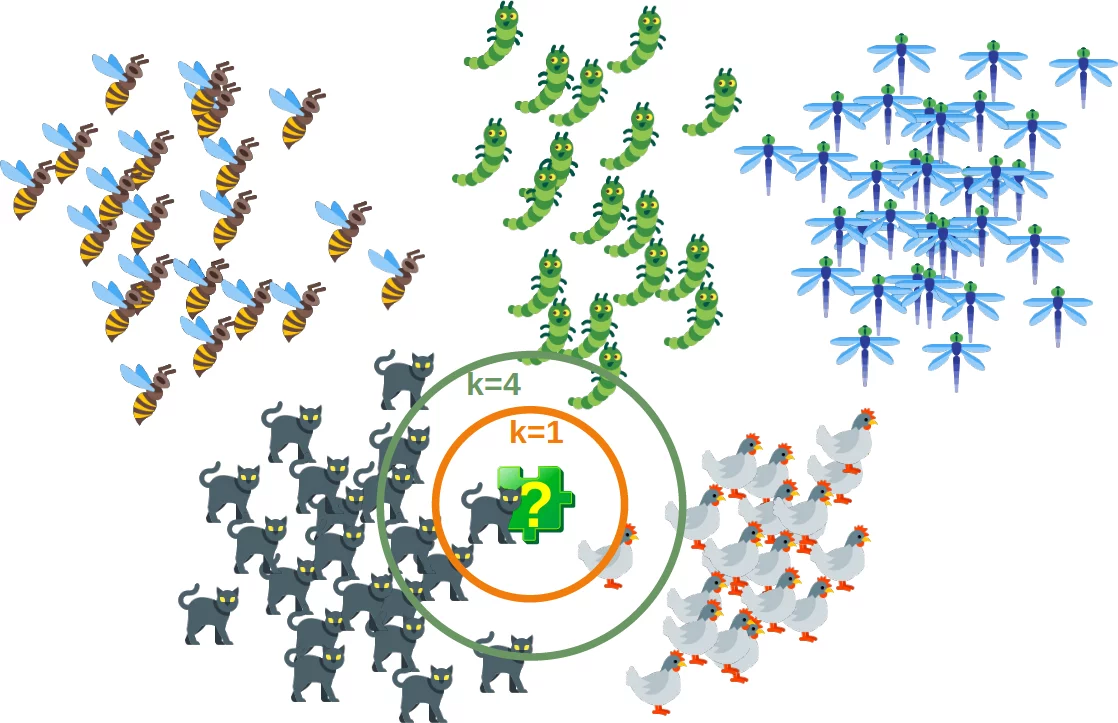
Das folgende Bild zeigt auf einfache Weise, wie der nächste Nachbar-Klassifikator funktioniert. Das Puzzleteil ist unbekannt. Um herauszufinden, welches Tier es sein könnte, müssen wir die Nachbarn finden. Wenn k = 1, ist der einzige Nachbarn eine Katze und wir nehmen in diesem Fall an, dass das Puzzleteil auch eine Katze sein sollte. Wenn k = 4 gilt, enthalten die nächsten Nachbarn ein Huhn und drei Katzen. In diesem Fall können wir annehmen, dass unser Objekt, also das Puzzleteil, eine Katze sein sollte.
k-Nächster-Nachbar von Grund auf¶
Dataset vorbereiten¶
Bevor wir einen Nearest-Neighbor Klassifikator schreiben, müssen wir über die Daten nachdenken, das heißt den Lern- und den Testdatensatz. Wir benutzen die "Iris"-Daten, die durch das sklearn-Modul zur Verfügung gestellt werden.
Der Datensatz beinhaltet 50 Beispiele von drei Arten von Schwertlilien (Englisch: Iris).
- Iris setosa (Borsten-Schwertlilie)
- Iris virginica und
- Iris versicolor (Verschiedenfarbige-Schwertlilie)
Vier Features (Merkmale) werden bei jeder Probe gemessen:
- Die Länge der Kelchblätter in Zentimeter
- Die Breite der Kelchblätter in Zentimeter
- Die Länge der Blütenblätter in Zentimeter
- Die Breite der Blütenblätter in Zentimeter
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
data = iris.data
labels = iris.target
for i in [0, 79, 99, 101]:
print(f"Index: {i:3}, Merkmale: {data[i]}, Label: {labels[i]}")
Erstellen wir ein Learnset aus den oben genannten Daten. Wir verwenden die Funktion permutation aus np.random um die Daten zufällig aufzuteilen.
# Seeding ist nur für die Website erforderlich,
# damit die Werte immer gleich sind:
np.random.seed(42)
indices = np.random.permutation(len(data))
n_training_samples = 12
learn_data = data[indices[:-n_training_samples]]
learn_labels = labels[indices[:-n_training_samples]]
test_data = data[indices[-n_training_samples:]]
test_labels = labels[indices[-n_training_samples:]]
print("Die ersten Stichproben unseres Lernsets:")
print(f"{'Index':7s}{'Daten':20s}{'Label':3s}")
for i in range(5):
print(f"{i:4d} {learn_data[i]} {learn_labels[i]:3}")
print("Die ersten Stichproben unseres Testsets:")
print(f"{'Index':7s}{'Daten':20s}{'Label':3s}")
for i in range(5):
print(f"{i:4d} {learn_data[i]} {learn_labels[i]:3}")
Der folgende Code dienst nur der Visualisierung der Daten aus dem Lernset. Unsere Daten bestehen aus vier Werten pro Schwertlilie. Um die Daten etwas zu reduzieren, summieren wir die dritten und vierten Werte auf. So können wir die Werte in einem 3-Dimensionalen Raum darstellen:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
X = []
for iclass in range(3):
X.append([[], [], []])
for i in range(len(learn_data)):
if learn_labels[i] == iclass:
X[iclass][0].append(learn_data[i][0])
X[iclass][1].append(learn_data[i][1])
X[iclass][2].append(sum(learn_data[i][2:]))
colours = ("r", "g", "y")
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for iclass in range(3):
ax.scatter(X[iclass][0], X[iclass][1], X[iclass][2], c=colours[iclass])
plt.show()
Entfernungsmetriken¶
Wir wir bereits ausführlich erwähnt haben, berechnen wir die Abstände zwischen den Punkten der Stichprobe und dem zu klassifizierenden Objekt. Zur Berechnung dieser Abstände benötigen wir eine Abstandsfunktion.
In n-dimensionalen Vektorräumen, benutzt man meistens einer der folgenden drei Abstandsmetriken:
Euklidischer-Abstand
Der euklidische Abstand zwischen zwei Punkten
xundyentweder in der Ebene oder im 3-dimensionalen Raum entspricht der Länge der Strecke, die diese beiden Punkte verbindet. Es kann aus den kartesischen Koordinaten der Punkte mit dem Satz des Pythagoras berechnet werden, daher wird es gelegentlich auch die Pythagoros-Entfernung bezeichnet. Die allgemeine Formel lautet:$$d(x, y) = \sqrt{\sum_{i=1}^{n} (x_i -y_i)^2}$$
Manhatten-Abstand
Es ist definiert als die Summe der absoluten Werte zwischen den Koordinaten von x und y : $$d(x, y) = \sum_{i=1}^{n} |x_i -y_i|$$
Minkowski-Abstand
Der Minkowski-Abstand verallgemeinert den Euklidischen und Manhatten-Abstand in einer Distanzmetrik. Wenn wir den Parameter
pin der folgenden Formel auf 1 einstellen, erhalten wir den Manhatten-Abstand, und mit dem Wert 2 erhalten wir den Euklidischen-Abstand: $$d(x, y) = { \left(\sum_{i=1}^{n} (x_i -y_i)^p \right)}^{\frac{1}{p}}$$
Das folgende Diagramm veranschaulicht den Zusammenhang zwischen Manhatten- und Euklidschem Abstand:
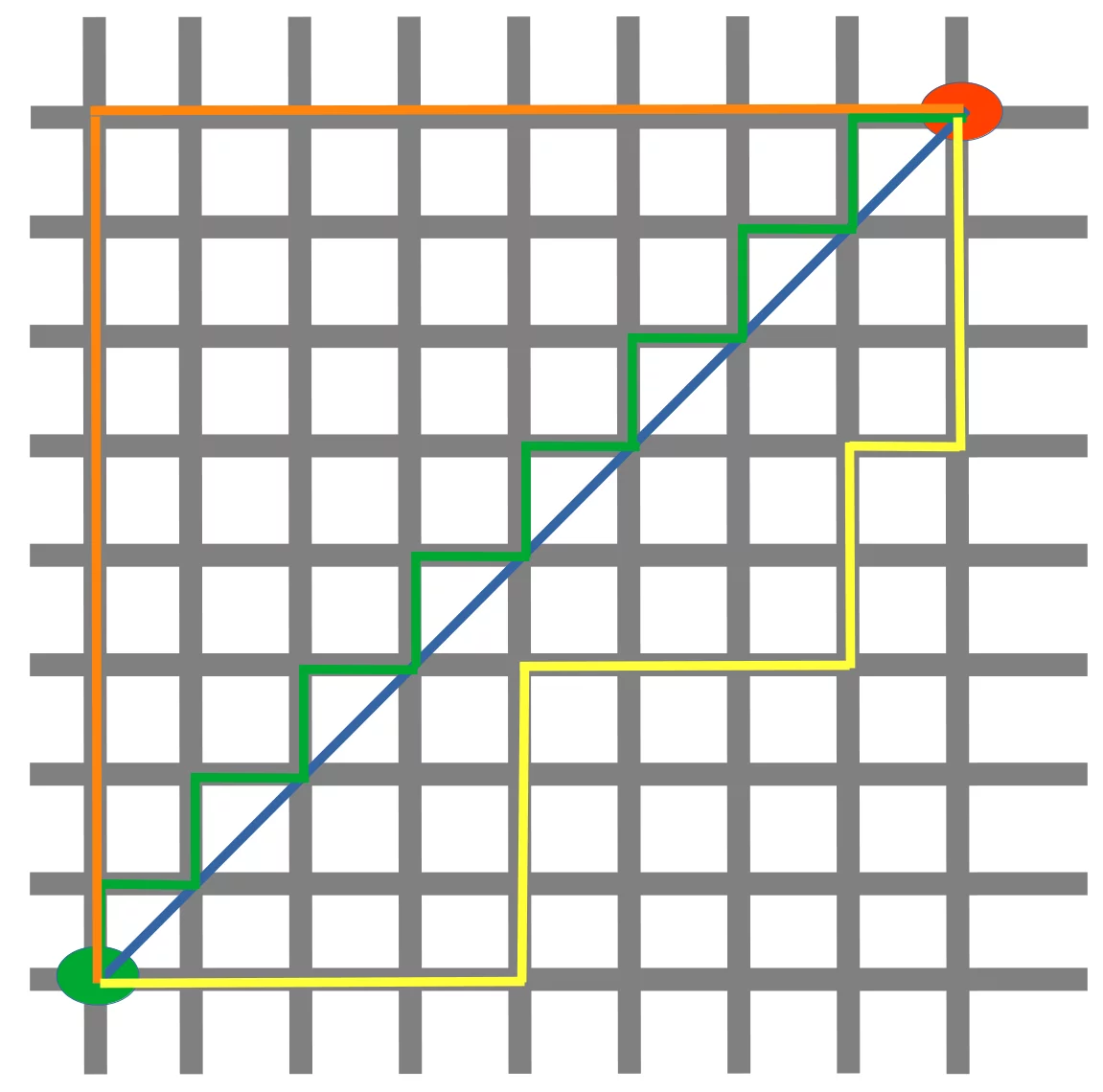
Die blaue Linie veranschaulicht den Euklidschen Abstand zwischen dem grünen und dem roten Punkt. Ansonsten kann man sich auch über die orange, grüne oder gelbe Linie vom grünen Punkt zum roten Punkt bewegen. Die Linien entsprechen der Manhatten-Distanz. Die Länge ist jeweils gleich.
Die Nachbarn ermitteln¶
Um Ähnlichkeiten zwischen zwei Objekten zu ermitteln brauchen wir eine Distanz-Funktion. In unserem Beispiel benutzen wir den Euklidischen Abstand.
Der euklidische Abstand zweier Punkte in der Ebene oder im Raum ist die zum Beispiel mit einem Lineal gemessene Länge einer Strecke, die diese zwei Punkte verbindet. In kartesischen Koordinaten kann der euklidische Abstand mit Hilfe des Satzes von Pythagoras berechnet werden. Mit Hilfe der so gewonnenen Formel kann der Begriff des euklidischen Abstands auf n-dimensionale Koordinatenräume verallgemeinert werden. Berechnen können wir den Abstand mit der Funktion norm aus dem Modul np.linalg:
def distance(instance1, instance2):
""" Berechnet den Eukliischen Abstand zwischen
zwei Instanzen"""
return np.linalg.norm(np.subtract(instance1, instance2))
print(distance([3, 5], [1, 1]))
print(distance(learn_data[3], learn_data[44]))
Die Funktion get_neighbors liefert eine Liste mit k Nachbarn zurück, die der Instanz test_instance am nächsten sind:
def get_neighbors(training_set,
labels,
test_instance,
k,
distance):
"""
get_neighbors berechnet eine Liste mit k-Nachbarn,
die der Instanz 'test_instance' am nächsten liegen.
'get_neighbors' liefert eine Liste mit k 3er-Tupel zurück.
Jedes Tupel besteht aus (index, dist, label), wobei gilt
index ist der Index aus training_set,
dist ist die Distanz zwischen der test_instance und der Instanz training_set[index]
distance ist eine Referenz auf die Funktion, welche die Distanz berechnet
"""
distances = []
for index in range(len(training_set)):
dist = distance(test_instance, training_set[index])
distances.append((training_set[index], dist, labels[index]))
distances.sort(key=lambda x: x[1])
neighbors = distances[:k]
return neighbors
Wir testen die Funktion mit unseren Iris-Proben:
for i in range(5):
neighbors = get_neighbors(learn_data,
learn_labels,
test_data[i],
3,
distance=distance)
print("Index: ",i,'\n',
"Testset-Data: ",test_data[i],'\n',
"Testset-Label: ",test_labels[i],'\n',
"Nachbarn: ",neighbors,'\n')
Voting für ein einzelnes Ergebnis¶
Wir schreiben eine Voting-Funktion (Abstimmung). Diese Funktion benutzt die Klasse Counter aus collections um die Anzahl der Klassen in einer Instanzen-Liste zu ermitteln. Die Instanzen-Liste stellt natürlich die Nachbarn dar. Die Funktion vote liefert die passendste Klasse zurück.
from collections import Counter
def vote(neighbors):
class_counter = Counter()
for neighbor in neighbors:
class_counter[neighbor[2]] += 1
return class_counter.most_common(1)[0][0]
Testen wir die vote Funktion mit unseren Trainings-Proben:
for i in range(n_training_samples):
neighbors = get_neighbors(learn_data,
learn_labels,
test_data[i],
3,
distance=distance)
print("Index: ", i,
", Ergebnis(vote): ", vote(neighbors),
", Bezeichnung: ", test_labels[i],
", Daten: ", test_data[i])
Wir sehen, dass die Vorhersagen mit den Bezeichnungen übereinstimmen, ausgenommen der Fall mit dem Index 8.
vote_prob ist eine Funktion wie vote, liefert aber den Klassen-Namen und dessen Wahrscheinlichkeit:
def vote_prob(neighbors):
class_counter = Counter()
for neighbor in neighbors:
class_counter[neighbor[2]] += 1
labels, votes = zip(*class_counter.most_common())
winner = class_counter.most_common(1)[0][0]
votes4winner = class_counter.most_common(1)[0][1]
return winner, votes4winner/sum(votes)
for i in range(n_training_samples):
neighbors = get_neighbors(learn_data,
learn_labels,
test_data[i],
5,
distance=distance)
print("Index: ", i,
", Ergebnis(vote_prob): ", vote_prob(neighbors),
", Bezeichnung: ", test_labels[i],
", Daten: ", test_data[i])
Der gewichtete Nearest-Neighbor-Klassifikator¶
Wir haben bis jetzt nur k Elemente aus der Nachbarschaft eines unbekannten Objektes "UO" betrachtet, und dessen Mehrheit. Die Mehrheit der Stimmabgaben hat sich im vorigen Beispiel stark gezeigt, wurde aber bei der folgenden Argumentation nicht berücksichtigt: "Je weiter ein Nachbar, desto mehr weicht er vom 'echten' Ergebnis ab."
Um es mit anderen Worten zu sagen: "Wir können dem nächsten Nachbarn mehr vertrauen als dem, der am weitesten entfernt ist." Nehmen wir an, dass das unbekannte Objekt "UO" 11 Nachbarn hat. Die naheliegendsten fünf Nachbarn gehören zur Klasse A und alle anderen sechs, die weiter entfernt sind, gehören zur Klasse B. Zu welcher Klasse wir "UO" wohl gehören? Das vorherige Vorgehen würde "Klasse B" sagen, denn wir haben ein Verhältnis von 6 zu 5 für Klasse B. Auf der anderen Seite gehören die naheliegendsten zur Klasse A und das sollte stärker berücksichtigt werden.
Um die Strategie weiterzuverfolgen, können wir den Nachbarn Gewichtungen zuweisen:
Der naheliegendste Nachbar einer Instanz erhält ein Gewicht von $1 / 1$, der zweitnächste bekommt ein Gewicht von $1 / 2$. Mit den weiteren Nachbarn wird ebenso weiterverfahren bis zu einem Gewicht von $1/k$ für den am weitesten entfernten Nachbarn.
Wir verwenden also die harmonische Serie als Gewichtung:
$$\sum_{i}^{k}{1/(i+1)} = 1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{k}$$
In der folgenden Funktion haben wir dies implementiert:
def vote_harmonic_weights(neighbors, all_results=True):
class_counter = Counter()
number_of_neighbors = len(neighbors)
for index in range(number_of_neighbors):
class_counter[neighbors[index][2]] += 1/(index+1)
labels, votes = zip(*class_counter.most_common())
#print(labels, votes)
winner = class_counter.most_common(1)[0][0]
votes4winner = class_counter.most_common(1)[0][1]
if all_results:
total = sum(class_counter.values(), 0.0)
for key in class_counter:
class_counter[key] /= total
return winner, class_counter.most_common()
else:
return winner, votes4winner / sum(votes)
for i in range(n_training_samples):
neighbors = get_neighbors(learn_data,
learn_labels,
test_data[i],
6,
distance=distance)
print("Index: ", i,
", Ergebnis(vote_harmonic_weights): ",
vote_harmonic_weights(neighbors,
all_results=True))
Das vorherige Vorgehen berücksichtigt lediglich die Reihenfolge der Nachbarn entsprechend der Entfernung. Wir können die Auswahl aber noch verbessern indem die aktuelle tatsächliche Entfernung berücksichtigt wird. Dafür schreiben wir eine neue Funktion:
def vote_distance_weights(neighbors, all_results=True):
class_counter = Counter()
number_of_neighbors = len(neighbors)
for index in range(number_of_neighbors):
dist = neighbors[index][1]
label = neighbors[index][2]
class_counter[label] += 1 / (dist**2 + 1)
labels, votes = zip(*class_counter.most_common())
#print(labels, votes)
winner = class_counter.most_common(1)[0][0]
votes4winner = class_counter.most_common(1)[0][1]
if all_results:
total = sum(class_counter.values(), 0.0)
for key in class_counter:
class_counter[key] /= total
return winner, class_counter.most_common()
else:
return winner, votes4winner / sum(votes)
for i in range(n_training_samples):
neighbors = get_neighbors(learn_data,
learn_labels,
test_data[i],
6,
distance=distance)
print("Index: ", i,
", Ergebnis(vote_distance_weights): ", vote_distance_weights(neighbors,
all_results=True))
Übung und Beispiel: Klassifizierung von Früchten mit K-Nächste-Nachbarn¶

Datensatz: Erzeugen Sie einen Datensatz mit Informationen über Früchte mit drei Merkmalen: Süße, Säuregehalt und Gewicht (in Gramm). Wir betrachten drei Arten von Früchten: "Apfel", "Zitrone", und "Mango".
Zielsetzung: Erstellen eines K-nearest neighbors Klassifikators zur Vorhersage der Obstsorte auf der Grundlage von Süße, Säuregehalt und Gewicht.
Zunächst werden wir Zufallsdaten mit Früchten und entsprechenden Daten erstellen:
Wir verwenden die [Brix-Skala] (https://en.wikipedia.org/wiki/Brix) für die Süße von Äpfeln.
import numpy as np
np.random.seed(42)
def create_features(number_samples, *min_max_features):
""" Creates an array with number_samples rows and len(min_max_features) columns """
features = []
for min_val, max_val,rounding in min_max_features:
features.append(np.random.uniform(min_val, max_val, number_samples).round(rounding))
result = np.column_stack(features)
return result
num_apples, num_mangos, num_lemons = 40, 42, 45
sweetness = (10, 18, 0)
acidity = 3.4, 4, 2
weight = 140.0, 250.0, 0
apples = create_features(num_apples, sweetness, acidity, weight)
apples
sweetness = (6, 14, 0)
acidity = 5.8, 6, 1
weight = 100.0, 300.0, 0
mangos = create_features(num_mangos, sweetness, acidity, weight)
sweetness = (6, 12, 0)
acidity = 2.0, 2.6, 1
weight = 130, 170, 0
lemons = create_features(num_lemons, sweetness, acidity, weight)
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# Combine the data and create labels
X = np.vstack((apples, mangos, lemons))
y = np.array(['Apple'] * num_apples + ['Mango'] * num_mangos + ['lemon'] * num_lemons)
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
n_test_samples = len(X_test)
for i in range(n_test_samples):
neighbors = get_neighbors(X_train,
y_train,
X_test[i],
6,
distance=distance)
print("index: ", i,
", result of vote: ",
vote_harmonic_weights(neighbors,
all_results=True))
Um unsere Klassifizierung zu bewerten, schreiben wir nun eine Bewertungsfunktion:
def evaluate(X_train, X_test, y_train, y_test, threshold=0):
"""
Bewertet die Leistung eines K-Nächste-Nachbarn-Klassifikators.
Parameter:
X_train (ndarray): Trainingsmerkmale.
X_test (ndarray): Test-Merkmale.
y_train (ndarray): Trainingsbezeichnungen.
y_test (ndarray): Testkennungen.
threshold (Float): Schwellenwert für die Entscheidungssicherheit (Standard: 0).
Wenn die Wahrscheinlichkeit der vorhergesagten Klasse unter diesem Schwellenwert liegt,
wird die Probe als 'undecided' (unentschieden) markiert.
Rückgabe:
dict: Ein Wörterbuch, das die Anzahl der richtigen Vorhersagen, falschen Vorhersagen
und unentschiedenen Vorhersagen beinhaltet
Anmerkung:
Die Funktion geht davon aus, dass es eine andere Funktion namens get_neighbors gibt, die
die k-nächsten Nachbarn für jede Stichprobe abruft, und die vom K-nearest neighbors-Algorithmus verwendete
vom K-Nächste-Nachbarn-Algorithmus verwendete Abstandsmaß ist in einer Variablen namens 'distance' definiert.
"""
evaluation = dict(corrects=0, wrongs=0, undecided=0)
n_test_samples = len(X_test)
for i in range(n_test_samples):
neighbors = get_neighbors(X_train,
y_train,
X_test[i],
6,
distance=distance)
class_label, probability = vote_distance_weights(neighbors, all_results=False)
if class_label == y_test[i]:
if probability >= threshold:
evaluation['corrects'] += 1
else:
evaluation['undecided'] += 1
else:
if probability >= threshold:
evaluation['wrongs'] += 1
else:
evaluation['undecided'] += 1
return evaluation
evaluate(X_train, X_test, y_train, y_test, 0.5)
evaluate(X_train, X_test, y_train, y_test, 0.9)
kNN in der Linguistik¶
Das nächste Beispiel kommt aus der Computer-Linguistik. Wir schauen uns an, wie wir mit einem k-Nearest-Neighbor-Klassifikator falsch geschriebene Worte erkennen können.
Dazu verwenden wir das Modul levenshtein, dass wir in unserem Tutorial zu Levenshtein Distanz bereits implementiert haben.
from levenshtein import levenshtein
cities = open("data/city_names.txt").readlines()
cities = [city.strip() for city in cities]
for city in ["Freiburg", "Frieburg", "Freiborg",
"Hamborg", "Sahrluis"]:
neighbors = get_neighbors(cities,
cities,
city,
2,
distance=levenshtein)
print("Ergebnis(vote_distance_weights): ", vote_distance_weights(neighbors))
Marvin und James führen uns in die Problematik des nächsten Beispiels ein:
Kannst du Marvin und James helfen?

Sie benötigen ein Englisch-Wörterbuch und einen k-nächsten-Nachbarn-Klassifikator, um das folgende Problem zu lösen.
Sollten Sie mit Linux (speziell Ubuntu) arbeiten, finden Sie eine Datei mit einem British-English-Wörterbuch unter /usr/share/dict/british-english. Ansonsten können Sie die Datei hier herunterladen (british-english.txt).
Wir verwenden im nächsten Beispiel Worte, die ziemlich falsch geschrieben sind. Wir sehen dass unsere einfache vote_prob Funktion gute Arbeit leistet, ausser in zwei Fällen: Bei der Korrektur von "holpposs" zu "helpless" und "blagrufoo" zu "barefoot". Während unsere vote_distance_weights Funktion in allen Fällen richtig korrigiert. Zugegeben, wir haben an "liberty" gedacht, als wir "liberdi" geschrieben haben. "liberal" ist aber auch eine gute Wahl.
words = []
with open("british-english.txt") as fh:
for line in fh:
word = line.strip()
words.append(word)
for word in ["holpful", "kundnoss", "holpposs", "thoes", "innerstand",
"blagrufoo", "liberdi"]:
neighbors = get_neighbors(words,
words,
word,
3,
distance=levenshtein)
print("vote_distance_weights: ", vote_distance_weights(neighbors,
all_results=False))
print("vote_prob: ", vote_prob(neighbors))
Nächstes Kapitel: Nächste Nachbarn-Klassifikation mit sklearn


 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen

