Metriken zu Evaluation

Einführen

Scharfschütze

Nicht nur beim maschinellen Lernen, sondern auch im allgemeinen Leben, insbesondere im Geschäftsleben, werden Sie Fragen wie "Wie genau ist Ihr Produkt?" oder "Wie präzise ist Ihre Maschine?" hören. Wenn Leute Antworten wie "Dies ist das genaueste Produkt auf seinem Gebiet!" oder "Diese Maschine hat die höchste vorstellbare Präzision!" erhalten, fühlen sich beide Antworten gut an. Sollten sie nicht? Wenn Sie beide Antworten gleichzeitig erhalten ja, aber jeweils eine alleine könnte problematisch sein. In der Tat werden die Begriffe "genau" und "präzise" sehr oft synonym verwendet. Wir werden später im Text genaue Definitionen geben, aber kurz gesagt können wir sagen: Genauigkeit ist ein Maß für die Nähe einiger Messungen zu einem bestimmten Wert, während Präzision die Nähe der Messungen zueinander ist.

Diese Begriffe sind auch beim maschinellen Lernen von äußerster Wichtigkeit. Wir brauchen sie zur Bewertung von ML-Algorithmen oder besser zu ihren Ergebnissen.

In diesem Kapitel unseres Python-Lernprogramms für maschinelles Lernen werden vier wichtige Metriken vorgestellt. Diese Metriken werden verwendet, um die Ergebnisse von Klassifizierungen auszuwerten.

Die Metriken sind:

  • Genauigkeit (engl. Accuracy)
  • Präzision (engl. precision)
  • Recall
  • F-Maß (englisch F1-score)

Wir werden jede dieser Metriken vorstellen und ihre Vor- und Nachteile diskutieren. Jede Metrik misst andere Aspekte der Leistung eines Klassifikators. Die Metriken sind für alle Kapitel unseres Tutorials zum maschinellen Lernen von größter Bedeutung.

Genauigkeit gegenüber Präzision

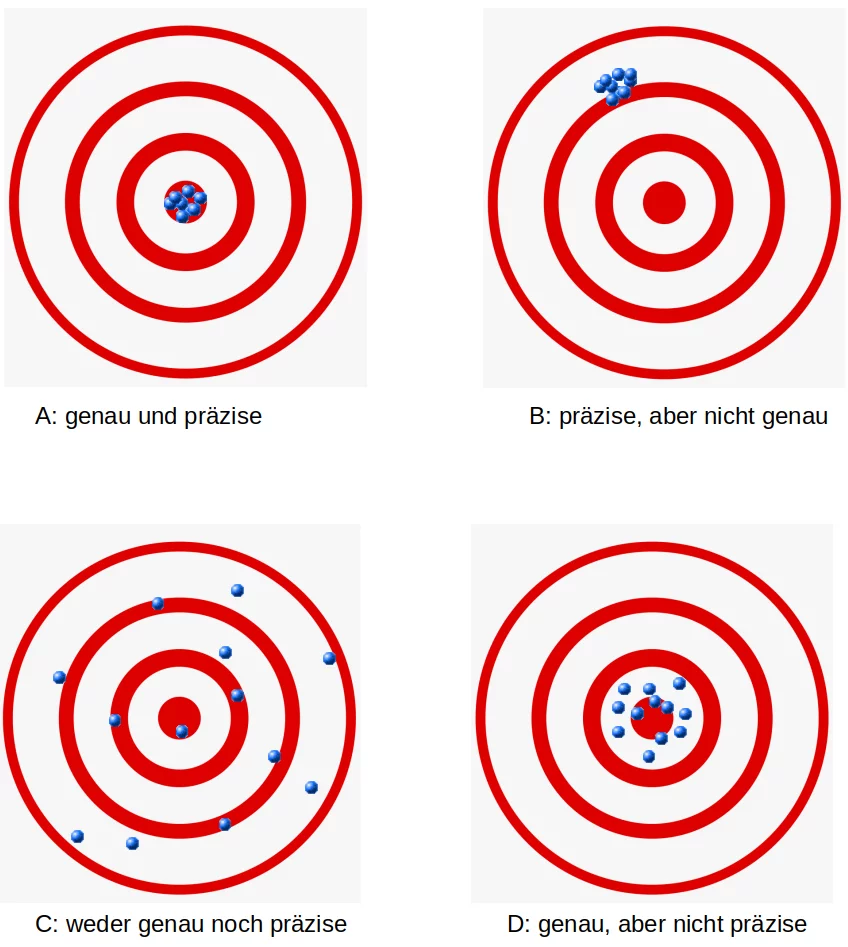
Die Genauigkeit ist ein Maß für die Nähe von Messungen zu einem bestimmten Wert (dem gewünschten Wert), während die Präzision ein Maß für die Nähe der Messungen zueinander ist, d.h. also nicht notwendig zu einem tatsächlichen oder gewünschten Wert. Mit anderen Worten: Wenn wir einen Satz von Datenpunkten aus wiederholten Messungen derselben Größe haben, wird der Satz als genau bezeichnet, wenn ihr Durchschnitt nahe am tatsächlichen Wert liegt. Andererseits nennen wir die Menge präzise, wenn die Messwerte nahe beieinander liegen, aber möglicherweise entfernt vom tatsächlichen Wert. Die beiden Konzepte sind unabhängig voneinander, was bedeutet, dass der Datensatz genau, präzise, präzise und genau oder keins von beides sein kann. Wir zeigen dies im folgenden Diagramm:

accuracy versus precision

Wahrheitsmatrix

Bevor wir mit dem Begriff "Genauigkeit" fortfahren, möchten wir sicherstellen, dass Sie verstehen, worum es in einer Wahrheitsmatrix, auch Konfusionsmatrix (englisch confusion matrx) genannt, geht.

Eine Konfusionsmatrix wird verwendet, um die Leistung eines Klassifikators zu visualisieren.

Die Spalten der Matrix repräsentieren die Instanzen der vorhergesagten Klassen und die Zeilen repräsentieren die Instanzen der tatsächlichen Klassen. (Hinweis: Es kann auch umgekehrt sein.)

Bei der binären Klassifizierung hat die Tabelle 2 Zeilen und 2 Spalten.

Wir wollen dieses Konzept mit einem Beispiel erläutern.

Beispiel:

Konfusionsmatrix
 Prognostizierte Klassen
Katze Hund
Tatsächliche
Klassen

 Katze 42 8
Hund 18 32

Dies bedeutet, dass der Klassifikator eine Katze in 42 Fällen korrekt vorhergesagt hat und 8 Katzeninstanzen fälschlicherweise als Hund vorhergesagt hat. Es wurden 32 Fälle als Hund korrekt vorhergesagt. 18 Fälle wurden fälschlicherweise als Katze statt als Hund vorhergesagt.

Genauigkeit bei der Klassifizierung

Wir interessieren uns für maschinelles Lernen und Genauigkeit wird auch als statistische Messgröße verwendet. Die Genauigkeit ist ein statistisches Maß, das als Quotient korrekter Vorhersagen (sowohl True Positives (TP) als auch True Negatives (TN)) eines Klassifikators geteilt durch die Summe aller vom Klassifikator gemachten Vorhersagen, einschließlich falsch Positive (FP) und falsch Negative (FN) definiert wird. Daher lautet die Formel zur Quantifizierung der binären Genauigkeit :

$$ Genauigkeit = {{TP + TN} \over {TP + TN + FP + FN}} $$

wobei gilt: TP = True positive; FP = False positive; TN = True negative; FN = False negative

Die dazugehörige Konfusionsmatrix sieht wie folgt aus:

Confusion
Matrix
 Vorhergesagte Klassen
negativ positiv
Tatsächliche
Klassen

 negativ TN FP
positiv FN TP

Wir werden nun die Genauigkeit für die Ergebnisse der Katzen- und Hundeklassifizierung berechnen. Anstelle von "richtig" und "falsch" sehen wir hier "Katze" und "Hund". Wir können die Genauigkeit so berechnen :

TP = 42
TN = 32
FP = 8
FN = 18
genauigkeit = (TP + TN)/(TP + TN + FP + FN)
print(genauigkeit)

0.74

Nehmen wir an, dass eir einen Klassifikator hätten, der immer "Hund" vorhersagt.

Konfusionsmtrix
 Vorhergesagte Klassen
Katze Hund
Actual
classes

 Katze 0 50
Hund 0 50

In diesem Fall haben wir eine Genauigkeit von 0.5:

TP, TN, FP, FN = 0, 50, 50, 0
genauigkeit = (TP + TN)/(TP + TN + FP + FN)
print(genauigkeit)

0.5

Genauigkeitsparadoxon

Wir werden das sogenannte Genauigkeitsparadoxon demonstrieren.

Ein Spam-Erkennungsklassifizierer wird durch die folgende Konfusionsmatrix beschrieben. Dabei steht "spam" für die Spam-Emails und "ham" für die guten Emails/p>

Konfusionsmatrix
 Vorhergesagte Klassen
spam ham
Tatsächliche
Klassen

 spam 4 1
ham 4 91 
TP, TN, FP, FN = 4, 91, 1, 4
genauigkeit = (TP + TN)/(TP + TN + FP + FN)
print(genauigkeit)

0.95

Der folgende Klassifikator sagt immer nur "ham" voraus und hat die gleich Genauigkeit.

Konfusionsmatrix
 Vorhergesagte Klassen
spam ham
Tatsächliche
Klassen

 spam 0 5
ham 0 95 
TP, TN, FP, FN = 0, 95, 5, 0
genauigkeit = (TP + TN)/(TP + TN + FP + FN)
print(genauigkeit)

0.95

Die Genauigkeit dieses Klassifikators beträgt 95%, obwohl er überhaupt keinen Spam erkennen kann.

Präzision

Präzision ist das Verhältnis der korrekt identifizierten positiven Fälle zu allen vorhergesagten positiven Fällen, d.h. den korrekten und falschen Fällen, die als "positiv" vorhergesagt wurden. Präzision ist der Anteil der abgerufenen Dokumente, die für die Abfrage relevant sind. Die Formel:

$$ präzision = {TP \over {TP + FP}}$$

Wir demonstrieren auch dies an einem Beispiel.

Konfusionsmatrix
 Vorhergesagte Klassen
spam ham
Tatsächliche
Klassen

 spam 12 14
ham 0 114

Wir können die "Präzision" für unser Beispiel berechnen:

TP = 114
FP = 14
# FN und TN werden in dieser Formel nicht benötigt!
präzision = TP / (TP + FP)
print(f"präzision: {präzision:4.2f}")

präzision: 0.89

Übung: Bevor Sie mit dem Text fortfahren, überlegen Sie, was der Wert "Präzision" bedeutet. Wenn Sie sich das Präzisionsmaß unseres Beispiels für Spamfilter ansehen, was sagt es Ihnen über die Qualität des Spamfilters aus? Wie sehen die Ergebnisse der Konfusionsmatrix eines idealen Spamfilters aus? Was ist schlimmer, hohe FP- oder FN-Werte?

Die Antworten finden Sie indirekt in den folgenden Erläuterungen.

NEbenbei gesagt: der ideale Spamfilter hätte 0 Werte für FP und FN.

Das vorherige Ergebnis bedeutet, dass 11 von hundert E-Mails als "ham" klassifiziert werden, obwohl es sich um Spam handelt. 89 sind korrekt als "ham" klassifiziert. Dies ist ein Punkt, an dem wir über die Kosten einer Fehlklassifizierung sprechen sollten. Es ist problematisch, wenn eine Spam-Mail nicht als "Spam" erkannt wird und uns stattdessen als "ham" präsentiert wird. Wenn der Prozentsatz nicht zu hoch ist, ist es ärgerlich, aber keine Katastrophe. Im Gegensatz dazu wird die E-Mail in vielen Fällen nicht angezeigt oder sogar automatisch gelöscht, wenn eine Nicht-Spam-Nachricht fälschlicherweise als Spam gekennzeichnet ist. Dies birgt beispielsweise ein hohes Risiko, Kunden und Freunde zu verlieren. Das Maß Präzision macht keine Aussage über diese zuletzt genannte Problemklasse. Wie sieht es mit anderen Maßen aus?

Wir werden uns recal und` `` F1-Score``` ansehen.

Recall

Recall, auch als Sensitivität bezeichnet, ist das Verhältnis der korrekt identifizierten positiven Fälle zu allen tatsächlichen positiven Fällen, d.h. die Summe der "Falsch Negativen" und "Richtig Positiven".

$$ recall = {TP \over {TP + FN}}$$ 
TP = 114
FN = 0
# FT (14) und TN (12) werden nicht benötigt!
recall = TP / (TP + FN)
print(f"recall: {recall:4.2f}")

recall: 1.00

The value 1 means that no non-spam message is wrongly labeled as spam. It is important for a good spam filter that this value should be 1. We have previously discussed this already.

F1-score

Das letzte Maß, dass wir untersuchen werden, ist der F1-score.

$$ F_1 = {2 \over {{1 \over recall} + {1 \over precision}}} = 2 \cdot {{{precision}\cdot{recall}} \over {{precision} + {recall}} }$$ 
TF = 7 # we set the True false values to 5 %
print("  FN    FP   TP     pre   acc   rec   f1")
for FN in range(0, 7):
    for FP in range(0, FN+1):
        # the sum of FN, FP, TF and TP will be 100:
        TP = 100 - FN - FP - TF
        #print(FN, FP, TP, FN+FP+TP+TF)
        precision = TP / (TP + FP)
        accuracy = (TP + TN)/(TP + TN + FP + FN)
        recall = TP / (TP + FN)
        f1_score = 2 * precision * recall / (precision + recall)
        print(f"{FN:6.2f}{FP:6.2f}{TP:6.2f}", end="")
        print(f"{precision:6.2f}{accuracy:6.2f}{recall:6.2f}{f1_score:6.2f}")

  FN    FP   TP     pre   acc   rec   f1
  0.00  0.00 93.00  1.00  1.00  1.00  1.00
  1.00  0.00 92.00  1.00  0.99  0.99  0.99
  1.00  1.00 91.00  0.99  0.99  0.99  0.99
  2.00  0.00 91.00  1.00  0.99  0.98  0.99
  2.00  1.00 90.00  0.99  0.98  0.98  0.98
  2.00  2.00 89.00  0.98  0.98  0.98  0.98
  3.00  0.00 90.00  1.00  0.98  0.97  0.98
  3.00  1.00 89.00  0.99  0.98  0.97  0.98
  3.00  2.00 88.00  0.98  0.97  0.97  0.97
  3.00  3.00 87.00  0.97  0.97  0.97  0.97
  4.00  0.00 89.00  1.00  0.98  0.96  0.98
  4.00  1.00 88.00  0.99  0.97  0.96  0.97
  4.00  2.00 87.00  0.98  0.97  0.96  0.97
  4.00  3.00 86.00  0.97  0.96  0.96  0.96
  4.00  4.00 85.00  0.96  0.96  0.96  0.96
  5.00  0.00 88.00  1.00  0.97  0.95  0.97
  5.00  1.00 87.00  0.99  0.97  0.95  0.97
  5.00  2.00 86.00  0.98  0.96  0.95  0.96
  5.00  3.00 85.00  0.97  0.96  0.94  0.96
  5.00  4.00 84.00  0.95  0.95  0.94  0.95
  5.00  5.00 83.00  0.94  0.95  0.94  0.94
  6.00  0.00 87.00  1.00  0.97  0.94  0.97
  6.00  1.00 86.00  0.99  0.96  0.93  0.96
  6.00  2.00 85.00  0.98  0.96  0.93  0.96
  6.00  3.00 84.00  0.97  0.95  0.93  0.95
  6.00  4.00 83.00  0.95  0.95  0.93  0.94
  6.00  5.00 82.00  0.94  0.94  0.93  0.94
  6.00  6.00 81.00  0.93  0.94  0.93  0.93

Wir können erkennen, dass der f1-score am Bestend das Worst-Case-Szenario refklektiert, dass der FN steigt, i.e. ham wird als spam klassifiziert!