Einfaches neuronales Netz

Linear separierbare Datensätze

Neuronales Netzwerk auf einem Ei

Wie wir im vorherigen Kapitel unseres Tutorials über maschinelles Lernen gezeigt haben, genügte ein neuronales Netzwerk, das nur aus einem Perzeptron besteht, um unsere Beispielklassen zu trennen. Natürlich haben wir diese Klassen sorgfältig entworfen, damit es funktioniert. Es gibt viele Klassen-Cluster, bei denen es nicht funktioniert. Wir werden uns einige andere Beispiele ansehen und Fälle diskutieren, in denen es nicht möglich ist, die Klassen zu trennen.

Unsere bisherigen Klassen waren linear separierbar. lineare Separierbarkeit ergibt Sinn in der euklidischen Geometrie. Zwei Mengen von Punkten (oder Klassen) in einer Ebene bezeichnet man als linear separierbar oder trennbar, wenn mindestens eine gerade Linie in der Ebene vorhanden ist, so dass sich alle Punkte der einen Klasse auf einer Seite der Linie und alle Punkte der anderen Klasse auf der anderen Seite befinden.

Etwas formaler:

Wenn zwei Datencluster (Klassen) durch eine Trennlinie in Form einer linearen Gleichung getrennt werden können $$\sum_{i=1}^{n} x_i \cdot w_i = 0$$

nennt man sie linear separierbar.

Andernfalls, falls eine solche Trennlinie nicht existiert, bezeichnet man die beiden Klassen als nicht linear separierbar. In diesem Fall können wir kein einfaches neuronales Netzwerk verwenden.

Perzeptron für die AND-Funktion

In unserem nächsten Beispiel programmieren wir ein einfaches Neuronales Netzwerk, welches die logische AND-Funktion implementiert. Sie hat zwei Eingaben und ist wie folgt definiert:

Eingabe1 Eingabe2 Ausgabe
0 0 0
0 1 0
1 0 0
1 1 1

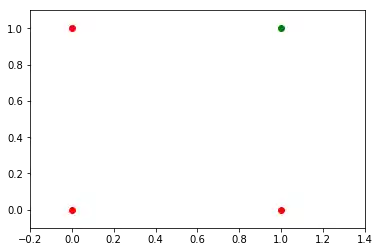
Wir haben im vorherigen Kapitel gelernt, dass ein neuronales Netzwerk mit einem Perzeptron und zwei Eingan als Trennlinie interpretiert werden kann, d. h. eine Gerade, die zwei Klassen teilt. Die beiden Klassen, die wir in unserem Beispiel klassifizieren möchten, sehen so aus:

In [1]:
import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots()
xmin, xmax = -0.2, 1.4
X = np.arange(xmin, xmax, 0.1)
ax.scatter(0, 0, color="r")
ax.scatter(0, 1, color="r")
ax.scatter(1, 0, color="r")
ax.scatter(1, 1, color="g")
ax.set_xlim([xmin, xmax])
ax.set_ylim([-0.1, 1.1])
m = -1
#ax.plot(X, m * X + 1.2, label="decision boundary")
plt.plot()
Out[1]:
[]
einfaches_neuronales_netz: Graph 0

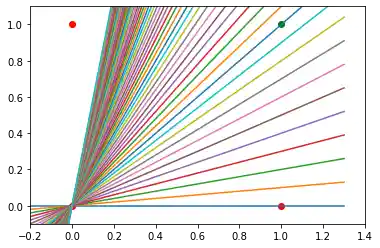
Wir haben auch herausgefunden, dass ein solches primitives neuronales Netzwerk nur in der Lage ist, Geraden durch den Ursprung zu beschreiben. Also Trennlinien der folgenden Art:

In [1]:
import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots()
xmin, xmax = -0.2, 1.4
X = np.arange(xmin, xmax, 0.1)
ax.set_xlim([xmin, xmax])
ax.set_ylim([-0.1, 1.1])
m = -1
for m in np.arange(0, 6, 0.1):
    ax.plot(X, m * X )
ax.scatter(0, 0, color="r")
ax.scatter(0, 1, color="r")
ax.scatter(1, 0, color="r")
ax.scatter(1, 1, color="g")
plt.plot()
Out[1]:
[]
einfaches_neuronales_netz 2: Graph 1

Wir können sehen, dass sich keine dieser Geraden als Trennlinie verwendet lässt. Keine Gerade durch den Ursprung ist dazu geeignet.

Wir brauchen eine Gerade

$$y = m \cdot x + c$$

wobei der Achsenabschnitt c verschieden von 0 ist.

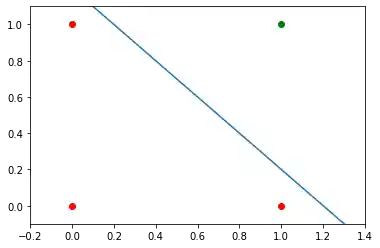
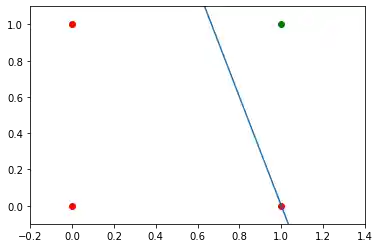
Die Gerade

$$y = -x + 1.2$$

könnte beispielsweise als Trennlinie für unser Problem verwendet werden:

In [2]:
import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots()
xmin, xmax = -0.2, 1.4
X = np.arange(xmin, xmax, 0.1)
ax.scatter(0, 0, color="r")
ax.scatter(0, 1, color="r")
ax.scatter(1, 0, color="r")
ax.scatter(1, 1, color="g")
ax.set_xlim([xmin, xmax])
ax.set_ylim([-0.1, 1.1])
m, c = -1, 1.2
ax.plot(X, m * X + c )
plt.plot()
Out[2]:
[]
einfaches_neuronales_netz 3: Graph 2

Es stellt sich die Frage, ob wir eine Lösung mit geringfügigen Modifikationen unseres Netzwerkmodells finden können? Oder mit anderen Worten: Können wir ein Perzeptron erstellen, welches in der Lage ist, beliebige Trennlinien zu finden?

Die Lösung besteht in der Zugabe eines Bias-Knotens.

Perzeptron mit Bias

Ein Perceptron mit zwei Eingangswerten und einem Bias-Wert entspricht einer allgemeinen Geraden. Mit Hilfe des Bias-Werts b können wir das Perzeptron so trainieren, dass es allgemeine Geraden (Trennlinien) mit von 0 verschiedenem Achsenabschnitt c beschreiben kann.

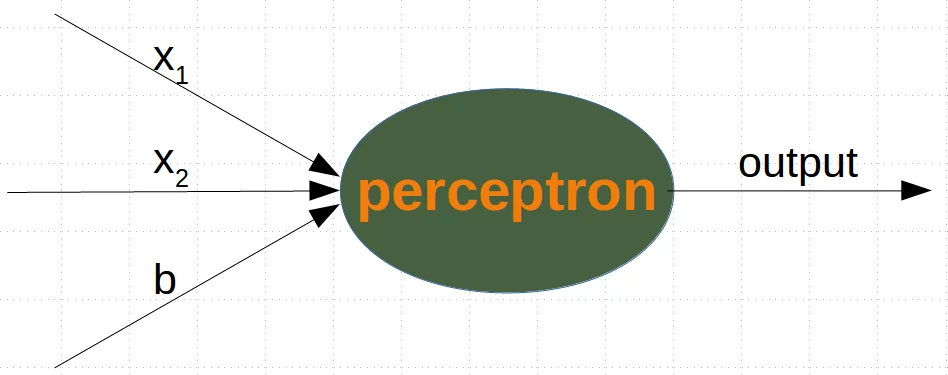
Ein Perzeptron mit zwei Eingaben und einem Bias-Wert

Während sich die Eingangswerte ändern können, bleibt der Bias-Wert immer konstant. Nur das Gewicht des Bias-Knotens kann angepasst werden.

Nun enthält die lineare Gleichung für ein Perzeptron einen Bias:

$$\sum_{i=1}^{n} w_i \cdot x_i + w_{n+1} \cdot b = 0$$

In unserem Fall schaut es wie folgt aus:

$$w_1 \cdot x_1 + w_2 \cdot x_2 + w_3 \cdot b= 0$$

dies ist äquivalent mit

$$ x_2 = -\frac{w_1}{w_2} \cdot x_1 - \frac{w_3}{w_2} \cdot b$$

Dies bedeutet:

$$m = -\frac{w_1}{w_2}$$

und

$$c = - \frac{w_3}{w_2} \cdot b$$

In [3]:
%%capture
%%writefile perceptrons.py
 
import numpy as np
from collections import Counter

class Perceptron:
    
    def __init__(self, 
                 weights,
                 bias=1,
                 learning_rate=0.3):
        """
        'weights' kann ein Numpy-Array, eine Liste oder ein 
        Tupel mit den Werten der Gewichte. Die Anzahl der Eingabewerte
         ist indirekt durch die Länge von 'weights' definiert 
        """
        self.weights = np.array(weights)
        self.bias = bias
        self.learning_rate = learning_rate
        
    @staticmethod
    def unit_step_function(x):
        if  x <= 0:
            return 0
        else:
            return 1
        
    def __call__(self, in_data):
        in_data = np.concatenate( (in_data, [self.bias]) )
        result = self.weights @ in_data
        return Perceptron.unit_step_function(result)
    
    def adjust(self, 
               target_result, 
               in_data):
        if type(in_data) != np.ndarray:
            in_data = np.array(in_data)  # 
        calculated_result = self(in_data)
        error = target_result - calculated_result
        if error != 0:
            in_data = np.concatenate( (in_data, [self.bias]) )
            correction = error * in_data * self.learning_rate
            self.weights += correction
            
    def evaluate(self, data, labels):
        evaluation = Counter()
        for sample, label in zip(data, labels):
            result = self(sample) # predict
            if result == label:
                evaluation["correct"] += 1
            else:
                evaluation["wrong"] += 1
        return evaluation

Wir gehen davon aus, dass der obige Python-Code mit der Perceptron-Klasse im aktuellen Arbeitsverzeichnis unter dem Namen 'perceptrons.py' gespeichert wird.

In [4]:
import numpy as np
from perceptrons import Perceptron

def labelled_samples(n):
    for _ in range(n):
        s = np.random.randint(0, 2, (2,))
        yield (s, 1) if s[0] == 1 and s[1] == 1 else (s, 0)

p = Perceptron(weights=[0.3, 0.3, 0.3],
               learning_rate=0.2)

for in_data, label in labelled_samples(30):
    p.adjust(label, 
             in_data)

test_data, test_labels = list(zip(*labelled_samples(30)))

evaluation = p.evaluate(test_data, test_labels)
print(evaluation)

Counter({'correct': 30})
In [6]:
import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots()
xmin, xmax = -0.2, 1.4
X = np.arange(xmin, xmax, 0.1)
ax.scatter(0, 0, color="r")
ax.scatter(0, 1, color="r")
ax.scatter(1, 0, color="r")
ax.scatter(1, 1, color="g")
ax.set_xlim([xmin, xmax])
ax.set_ylim([-0.1, 1.1])
m = -p.weights[0] / p.weights[1]
c = -p.weights[2] / p.weights[1]
print(m, c)
ax.plot(X, m * X + c )
plt.plot();

-3.0000000000000004 3.0000000000000013
einfaches_neuronales_netz 4: Graph 3

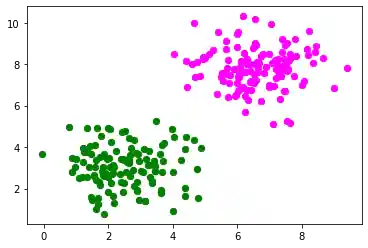
Wir erstellen ein anderes Beispiel mit linear trennbaren Datensätzen, für die wir auch einen Bias-Knoten zur Trennung benötigen. Wir werden die make_bobs-Funktion von sklearn.datasets dazu benutzen:

In [7]:
from sklearn.datasets import make_blobs

n_samples = 250
samples, labels = make_blobs(n_samples=n_samples, 
                             centers=([2.5, 3], [6.7, 7.9]), 
                             random_state=0)

Wir werden nun die vorher erzeugten Daten visualisieren:

In [8]:
import matplotlib.pyplot as plt

colours = ('green', 'magenta', 'blue', 'cyan', 'yellow', 'red')
fig, ax = plt.subplots()


for n_class in range(2):
    ax.scatter(samples[labels==n_class][:, 0], samples[labels==n_class][:, 1], 
               c=colours[n_class], s=40, label=str(n_class))
einfaches_neuronales_netz 5: Graph 4
In [9]:
n_learn_data = int(n_samples * 0.8) # 80 % of available data points
learn_data, test_data = samples[:n_learn_data], samples[-n_learn_data:]
learn_labels, test_labels = labels[:n_learn_data], labels[-n_learn_data:]

from perceptrons import Perceptron

p = Perceptron(weights=[0.3, 0.3, 0.3],
               learning_rate=0.8)

for sample, label in zip(learn_data, learn_labels):
    p.adjust(label,
             sample)

evaluation = p.evaluate(learn_data, learn_labels)
print(evaluation)

Counter({'correct': 200})

Nun wollen wir auch die Trennlinie darstellen:

In [10]:
import matplotlib.pyplot as plt


fig, ax = plt.subplots()

# plotting learn data
colours = ('green', 'blue')
for n_class in range(2):
    ax.scatter(learn_data[learn_labels==n_class][:, 0], 
               learn_data[learn_labels==n_class][:, 1], 
               c=colours[n_class], s=40, label=str(n_class))
    
# plotting test data
colours = ('lightgreen', 'lightblue')
for n_class in range(2):
    ax.scatter(test_data[test_labels==n_class][:, 0], 
               test_data[test_labels==n_class][:, 1], 
               c=colours[n_class], s=40, label=str(n_class))


    
X = np.arange(np.max(samples[:,0]))
m = -p.weights[0] / p.weights[1]
c = -p.weights[2] / p.weights[1]
print(m, c)
ax.plot(X, m * X + c )
plt.plot()
plt.show()

-1.5513529034664024 11.736643489707035
einfaches_neuronales_netz 6: Graph 5

Im folgenden Abschnitt werden wir das XOR-Problem für neuronale Netzwerke einführen. Es ist das einfachste Beispiel eines nicht linear trennbaren neuronalen Netzwerks. Es kann mit einer zusätzlichen Neuronenschicht gelöst werden, die als verborgene Schicht (hidden layer) bezeichnet wird.

Das XOR-Problem für neuronale Netze

Die XOR-Funktion wird durch folgende Tabelle definiert:

Eingabe1 Eingabe2 XOR-Ausgabe
0 0 0
0 1 1
1 0 1
1 1 0

Dieses Problem kann nicht mit einem einfachen Netzwerk gelöst werden, wie wir in folgendem Diagramm sehen können:

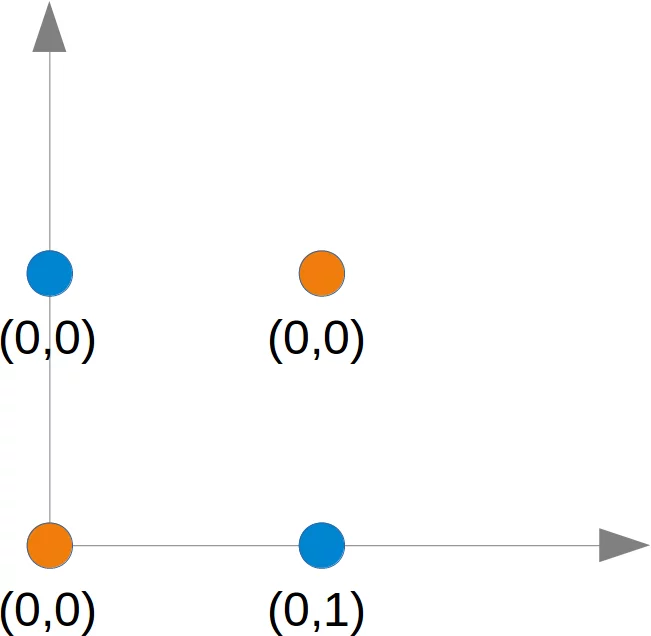
XOR-Problem in der Ebene

Egal welche Gerade man wählt, es wird einem niemals gelingen, die blauen Punkte auf einer Seite und den orangefarbenen Punkten auf der anderen Seite zu haben. Dies ist in der folgenden Abbildung dargestellt. Die orangefarbenen Punkte befinden sich auf der orangefarbenen Linie. Dies bedeutet, dass dies keine Trennlinie sein kann. Wenn wir diese Zeile parallel bewegen - egal in welche Richtung, es gibt immer zwei orangefarbene und einen blauen Punkt auf einer Seite und nur einen blauen Punkt auf der anderen Seite. Wenn wir die orangefarbene Linie nicht parallel bewegen, gibt es auf beiden Seiten einen blauen und einen orangefarbenen Punkt, außer wenn die Linie einen orangefarbenen Punkt durchläuft. Es gibt also keine Möglichkeit, dass eine einzige gerade Linie diese Punkte trennen kann.

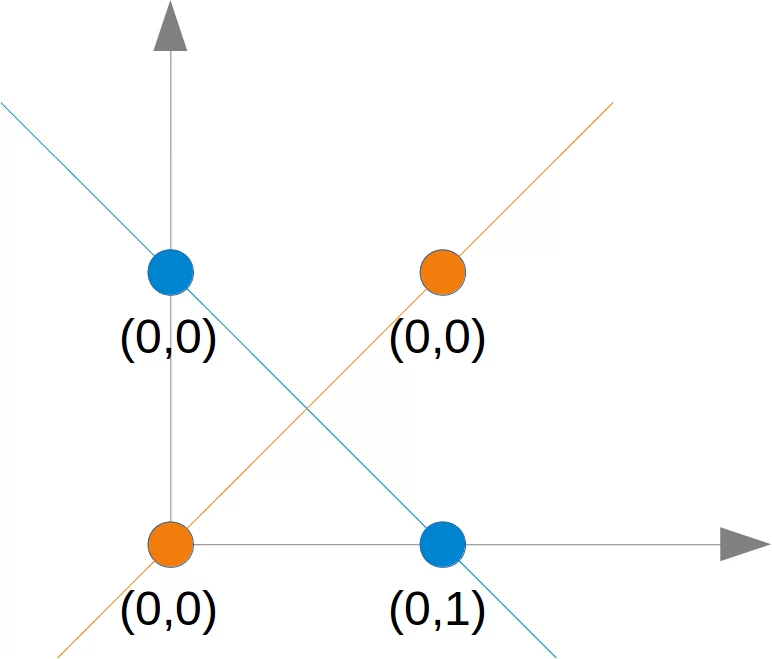
Keine Trennlinie für das XOR-Problem

Um dieses Problem zu lösen, müssen wir eine neue Art von neuronalen Netzwerken einführen, ein Netzwerk mit sogenannten verborgenen Schichten (hidden layers). Eine verborgene Schicht ermöglicht es dem Netzwerk, die Eingabedaten neu zu organisieren oder neu anzuordnen.

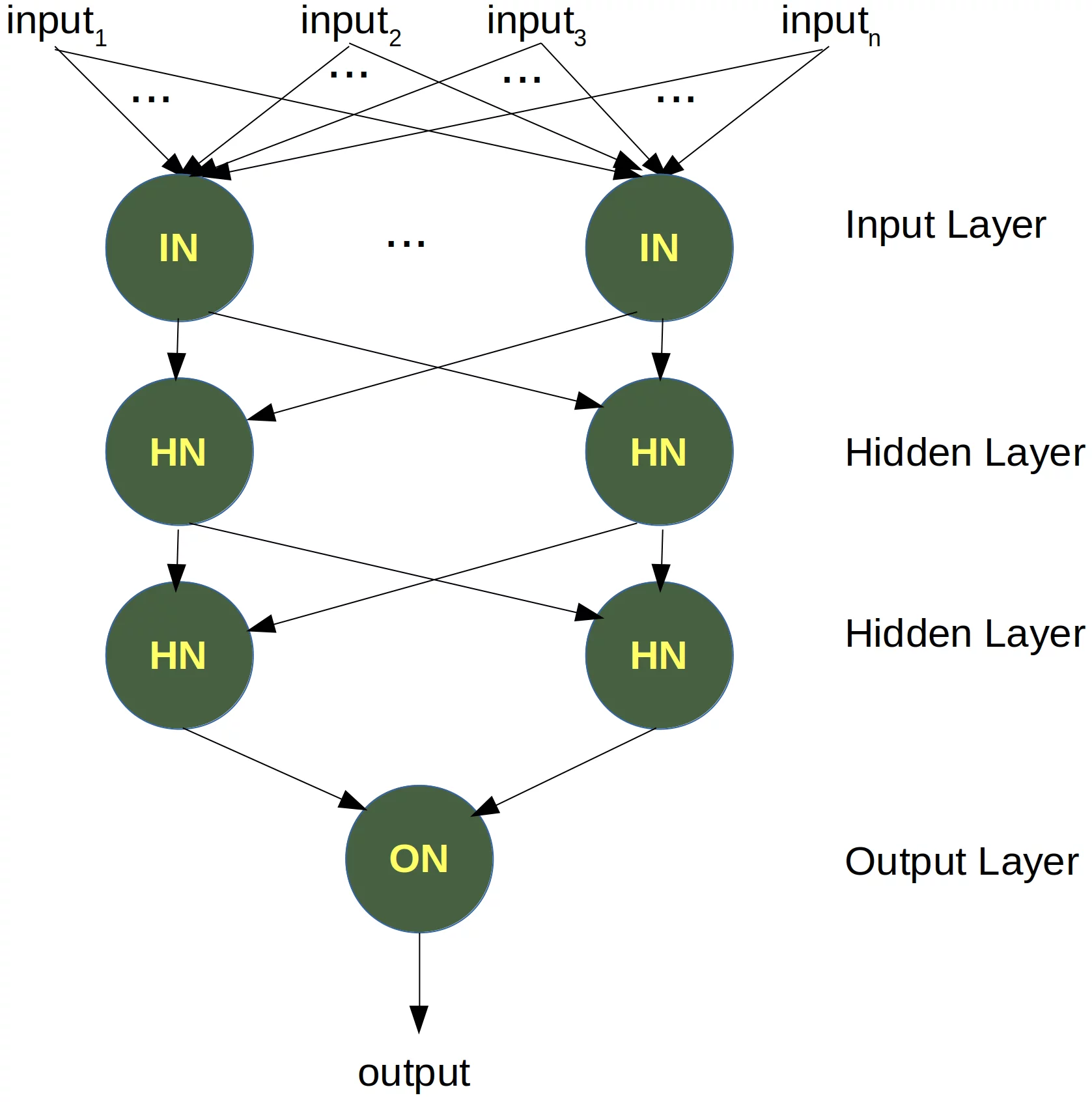
Simple artificial network with hidden layers

Wir benötigen nur eine verborgene Schicht mit zwei Neuronen. Eine arbeitet wir ein AND-Gatter und die andere wie ein OR-Gatter. Die Ausgabe "feuert", wenn das OR-Gatter feuert und das AND-Gatter nicht.

Wie bereits erwähnt, können wir keine Trennlinie finden, die die orangefarbenen Punkte von den blauen Punkten trennt. Sie können jedoch durch zwei Linien getrennt werden, z. B. L1 und L2 in dem folgenden Diagramm:

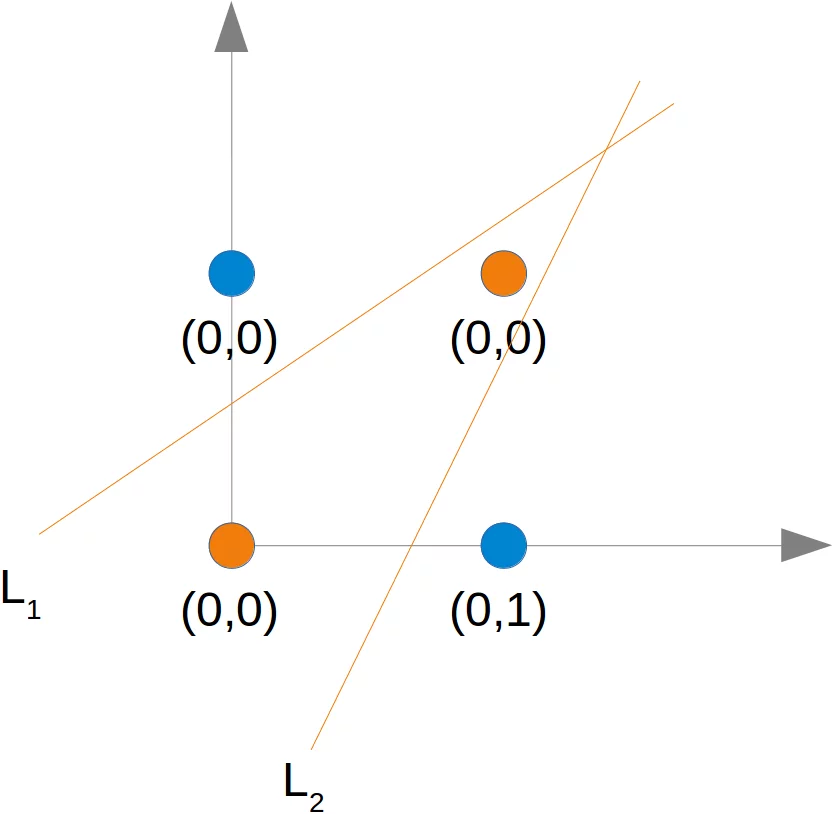
XOR problem in neural networks

Um dieses Problem zu lösen benötigen wir ein Netzwerk der folgenden Art, d. h. eines mit einer verborgenen Schicht N1 und N2

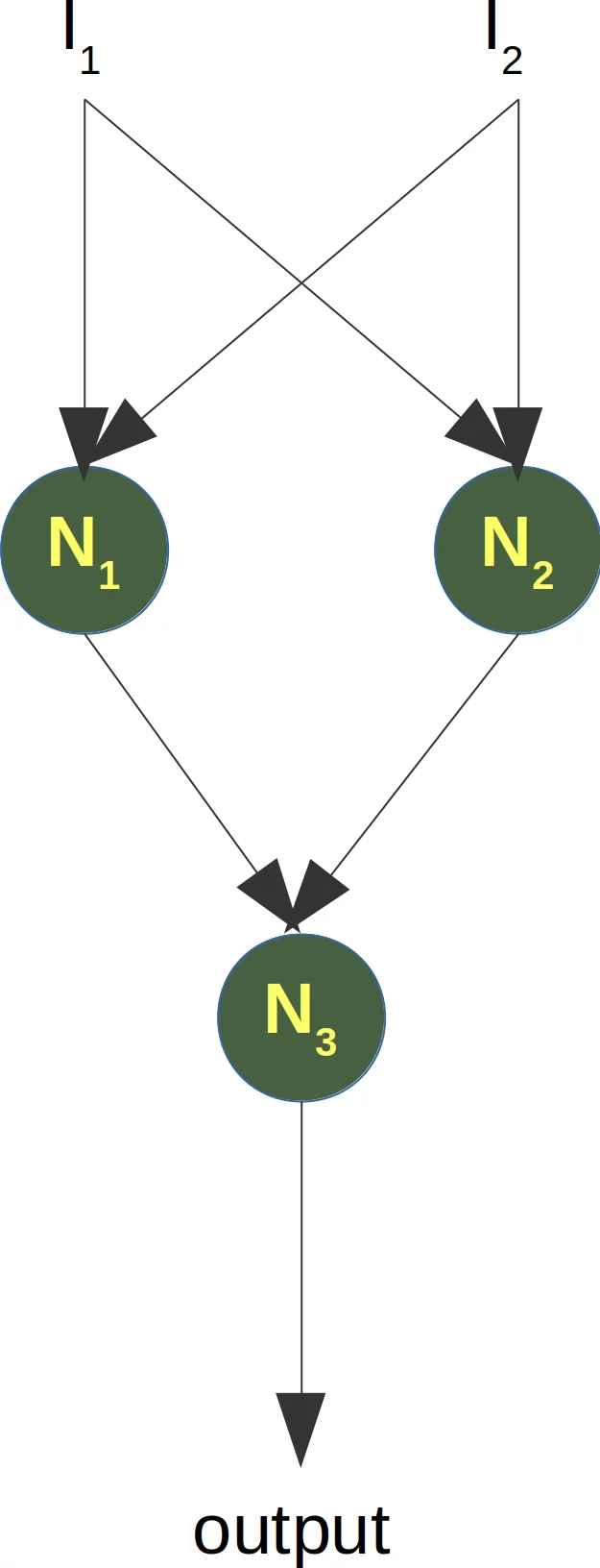
network solving the xor problem

Das Perzeptron N1 bestimmt eine Trennlinie, z. B. L1 und das Perzeptron N2 bestimmt die andere Trennlinie L2. N3 löst dann unser Problem:

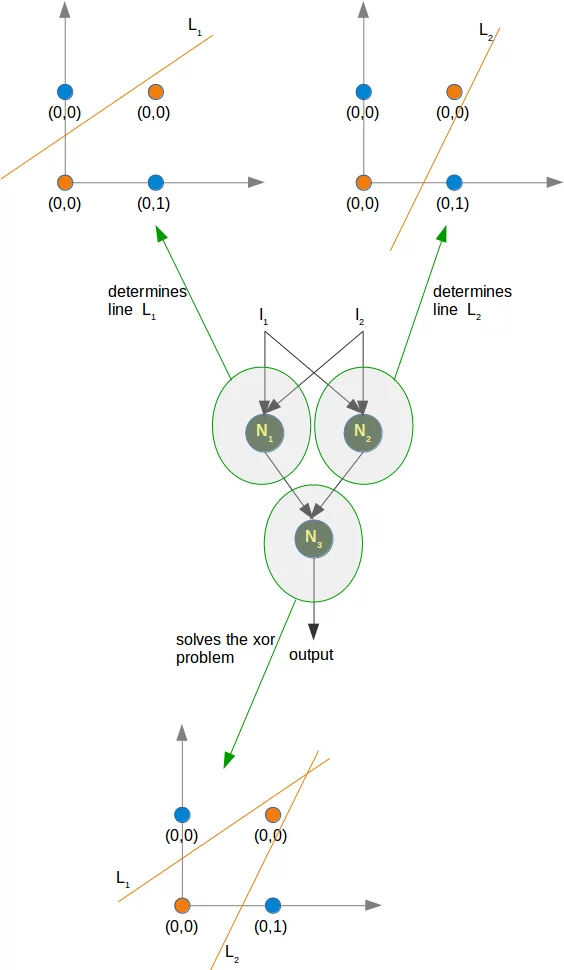
Explaining the network solving the xor problem

Die Implementierung von diesem Netzwerk muss bis zum nächsten Kapitel unseres Turorials über maschinelles Lernen warten.

Aufgaben

Aufgabe 1

Erweitere die AND-Funktion, dass sie Fließkommazahlen zwischen 0 und 1 in der folgenden Art zurückliefert:

Input1 Input2 Output
x1 < 0.5 x2 < 0.5 0
x1 < 0.5 x2 >= 0.5 0
x1 >= 0.5 x2 < 0.5 0
x1 >= 0.5 x2 >= 0.5 1

Versuche ein neuronales Netzwerk mit nur einem Perzeptron zu trainieren. Warum funktioniert dies nicht?

Aufgabe 2

Ein Punkt gehört zu einer Klasse 0, falls $x_1 < 0.5$ ist und gehört zur Klasse 1, falls $x_1 >= 0.5$ ist. Trainiere ein Netzwerk mit einem Perzeptron, um beliebige Punkte zu trainieren. Was kann man über die Trennlinie sagen? Was über die Eingabewerte?

Lösungen zu den Aufgaben

Lösung zur ersten Aufgabe

In [15]:
from perceptrons import Perceptron

p = Perceptron(weights=[0.3, 0.3, 0.3],
               bias=1,
               learning_rate=0.2)

def labelled_samples(n):
    for _ in range(n):
        s = np.random.random((2,))
        yield (s, 1) if s[0] >= 0.5 and s[1] >= 0.5 else (s, 0)

for in_data, label in labelled_samples(100):
    p.adjust(label, 
             in_data)

test_data, test_labels = list(zip(*labelled_samples(120)))

evaluation = p.evaluate(test_data, test_labels)
print(evaluation)

Counter({'wrong': 61, 'correct': 59})

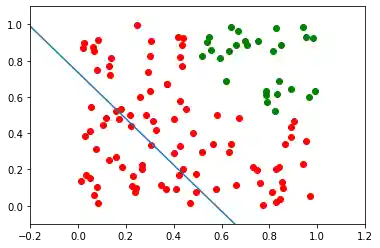
Der einfachste Weg zu sehen, dass es nicht funktioniert kann, besteht darin, die Daten zu visualisieren:

In [16]:
import matplotlib.pyplot as plt
import numpy as np

ones = [test_data[i] for i in range(len(test_data)) if test_labels[i] == 1]
zeroes = [test_data[i] for i in range(len(test_data)) if test_labels[i] == 0]

fig, ax = plt.subplots()
xmin, xmax = -0.2, 1.2
X, Y = list(zip(*ones))
ax.scatter(X, Y, color="g")
X, Y = list(zip(*zeroes))
ax.scatter(X, Y, color="r")
ax.set_xlim([xmin, xmax])
ax.set_ylim([-0.1, 1.1])
c = -p.weights[2] / p.weights[1]
m = -p.weights[0] / p.weights[1]
X = np.arange(xmin, xmax, 0.1)
ax.plot(X, m * X + c, label="decision boundary")
Out[16]:
[<matplotlib.lines.Line2D at 0x7fdfd17fd6d0>]
einfaches_neuronales_netz 7: Graph 6

Wir können erkennen, dass sich die grünen und die roten Punkte nicht durch eine Gerade trennen lassen. We can see that the green points and the red points are not separable by one straight line.

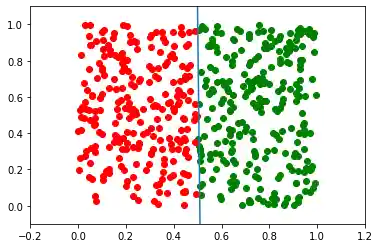
Lösung zur zweiten Aufgabe

In [17]:
from perceptrons import Perceptron

import numpy as np
from collections import Counter

def labelled_samples(n):
    for _ in range(n):
        s = np.random.random((2,))
        yield (s, 0) if s[0] < 0.5 else (s, 1)


p = Perceptron(weights=[0.3, 0.3, 0.3],
               learning_rate=0.4)

for in_data, label in labelled_samples(300):
    p.adjust(label, 
             in_data)

test_data, test_labels = list(zip(*labelled_samples(500)))

print(p.weights)
p.evaluate(test_data, test_labels)

[ 1.76735883  0.01530388 -0.9       ]
Out[17]:
Counter({'correct': 499, 'wrong': 1})
In [18]:
import matplotlib.pyplot as plt
import numpy as np

ones = [test_data[i] for i in range(len(test_data)) if test_labels[i] == 1]
zeroes = [test_data[i] for i in range(len(test_data)) if test_labels[i] == 0]

fig, ax = plt.subplots()
xmin, xmax = -0.2, 1.2
X, Y = list(zip(*ones))
ax.scatter(X, Y, color="g")
X, Y = list(zip(*zeroes))
ax.scatter(X, Y, color="r")
ax.set_xlim([xmin, xmax])
ax.set_ylim([-0.1, 1.1])
c = -p.weights[2] / p.weights[1]
m = -p.weights[0] / p.weights[1]
X = np.arange(xmin, xmax, 0.1)
ax.plot(X, m * X + c, label="decision boundary")
Out[18]:
[<matplotlib.lines.Line2D at 0x7fdfd17e29d0>]
einfaches_neuronales_netz 8: Graph 7
In [21]:
p.weights, m
Out[21]:
(array([ 2.03831116, -0.1785671 , -0.9       ]), 11.414819026425487)

Die Steigung m wird steiler und steiler in solchen Situation, d. h. strebt gegen Unendlich.