Informationen zum Buch
Turingmaschine
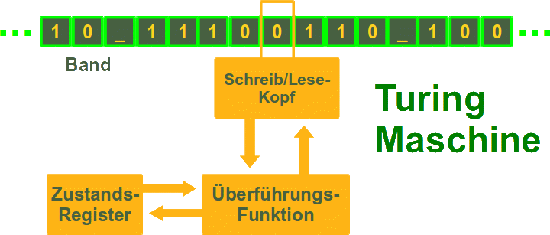Um es gleich zu sagen: Die Turingmaschine (TM) ist keine Maschine. Sie ist vielmehr ein mathematisches Modell, was
der englische Mathematiker Alan Turing im Jahre 1936 formuliert hatte. Aber es handelt sich um ein mathematisches
Modell, das ein einfaches Modell eines Computers beschreibt. Ein Modell, dass in der Lage ist alle Programme von jedem
realen Computer zu modellieren. Die Turingmaschine dient in der theoretischen Informatik zwei Zielen:
- Mit Hilfe der TM eine Klasse von Sprachen zu definieren, d.h. strukturiert oder rekursiv aufzählbare Sprachen.
- Zur Definition der partiell rekursiven Funktionen
Formale Definition der Turingmaschine
Eine deterministische Turingmaschine kann man als 7-TupelM = (Q, Σ, Γ, δ, b, q0, qf)
definieren mit
- Q ist eine endliche Zustandsmenge
- Γ ist das endliche Band-Alphabet
- Σ ist das endliche Eingabealphabet mit Σ ⊂ Γ
- δ ist die Überführungsfunktion:
δ : (Q \ {qf}) x Γ → Q x Γ x {L,N,R} - b ∈ &Gamma \ Σ bezeichnet ein leeres Feld
- q0 ∈ Q ist der Anfangszustand
- qf ∈ Q ist die Menge der möglichen End-Zustände
Beispiel: Berechnung des binären Komplementes
Wir definieren ("programmieren") eine Turingmaschine, die in der Lage ist die binäre Eingabe auf dem Eingabeband in ihr binäres Komplement zu wandeln. Die Eingabe "1100111" wird so beispielsweise in "0011000" gewandelt.Σ = {0, 1}
Q = {init, final}
q0 = init
qf = final
| Funktion | Beschreibung |
|---|---|
| δ(init,0) = (init, 1, R) | Wenn sich die Maschine in dem Zustand "init" befindet und eine 0 vom Schreib-Lesekopf gelesen wird, wird eine 1 zurückgeschrieben und sie geht in den Zustand "init" (der Zustand bleibt also unverändert) über. Danach wird der Kopf ein Feld nach rechts bewegt. |
| δ(init,1) = (init, 0, R) | Wenn sich die Maschine in dem Zustand "init" befindet und eine 1 vom Schreib-Lesekopf gelesen wird, wird eine 0 zurückgeschrieben und sie geht in den Zustand "init" (der Zustand bleibt also unverändert) über. Danach wird der Kopf ein Feld nach rechts bewegt. |
| δ(init,b) = (final, b, N) | Wenn ein Leerzeichen ("b") gelesen wird, was dem Ende der Eingabe einspricht, geht die TM in den Endzustand "final" über und hält. |
Implementierung einer Turingmaschine in Python
Wir realisieren eine Turingmaschine in Python als Klasse. Für das Band dieser Turingmaschine definieren wir eine eigene Klasse. Das Band setzen wir intern als Dictionary mit Integers als Schlüssel um, die positiv und negativ sein können. Dies ist notwendig, da Bänder von Turingmaschinen beidseitig unbeschränkt sind. Eine normale Python-Liste erfüllt diese Eigenschaft nicht, da sie durch den Index 0 einseitig beschränkt ist.In der Klasse Tape definieren wir die Methode method __str__(self), die von der eingebauten (built-in) str()-Funktion aufgerufen wird und von der print-Funktion benutzt wird, um die "informelle" String-Darstellung eines Objektes zu berechnen, in unserem Fall die Darstellung eines Bandes (Tape). Von dieser Möglichkeit wird in der print-Anweisung der Methode show_tape() von Klasse TuringMachine Gebrauch gemacht.
Die Methode __getitem__() ermöglicht den lesenden Zugriff mittels Indizes auf das Band. Die Methode __setitem() ist nötig, damit auch ein schreibender Zugriff möglich ist, wie beispielsweise in der Anweisung "
self.__tape[self.__head_position] = y[1]"
class Tape(object):
blank_symbol = " "
def __init__(self,
input=""):
self.__tape = {}
for i in range(len(input)):
self.__tape[i] = input[i]
def __str__(self):
s = ""
min_used_index = min(self.__tape.keys())
max_used_index = max(self.__tape.keys())
for i in range(min_used_index,max_used_index):
s += self.__tape[i]
return s
def __getitem__(self,index):
if index in self.__tape:
return self.__tape[index]
else:
return blank_symbol
def __setitem__(self, pos, char):
self.__tape[pos] = char
class TuringMachine(object):
def __init__(self,
tape = "",
blank_symbol = " ",
tape_alphabet = ["0", "1"],
initial_state = "",
accepting_states = [],
final_states = [],
transition_function = {}):
self.__tape = Tape(tape)
self.__head_position = 0
self.__blank_symbol = blank_symbol
self.__current_state = initial_state
self.__transition_function = transition_function
self.__tape_alphabet = tape_alphabet
self.__final_states = final_states
def show_tape(self):
print(self.__tape)
return True
def step(self):
char_under_head = self.__tape[self.__head_position]
x = (self.__current_state, char_under_head)
if x in self.__transition_function:
y = self.__transition_function[x]
self.__tape[self.__head_position] = y[1]
if y[2] == "R":
self.__head_position += 1
elif y[2] == "L":
self.__head_position -= 1
self.__current_state = y[0]
def final(self):
if self.__current_state in self.__final_states:
return True
else:
return False
Benutzung der Klasse TuringMachine:
from turing_machine import TuringMachine
initial_state = "init",
accepting_states = ["final"],
transition_function = {("init","0"):("init", "1", "R"),
("init","1"):("init", "0", "R"),
("init"," "):("final"," ", "N"),
}
final_states = ["final"]
t = TuringMachine("010011 ",
initial_state = "init",
final_states = final_states,
transition_function=transition_function)
print("Input on Tape:")
t.show_tape()
while not t.final():
t.step()
print("Result of the Turing machine calculation:")
t.show_tape()
Unser Programm liefert die folgende Ausgabe:
Input on Tape: 010011 Result of the Turing machine calculation: 101100