Informationen zum Buch
Voriges Kapitel: Pipe, Pipes und "99 Bottles of Beer"
Nächstes Kapitel: Ein Beispiel für Rekursion: Türme von Hanoi
Nächstes Kapitel: Ein Beispiel für Rekursion: Türme von Hanoi
Graphen in Python
Ursprünge der Graphen-Theorie
Bevor wir mit der eigentlichen Implementierung von Graphen in Python beginnen und bevor wir
ein Python-Modul einführen, die Graphen implementieren, wollen wir uns mit den Ursprüngen der
Graphen-Theorie ein wenig beschäftigen.
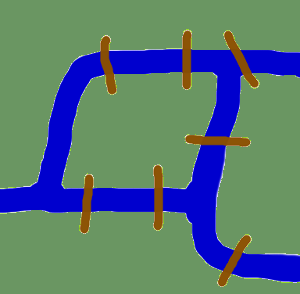
Dazu müssen wir uns ins Königsberg des 18. Jahrhunderts begeben. Damals war Königsberg eine Stadt in Preußen. Die Pregel floss durch die Stadt und schloss zwei Inseln ein. Die durch den Fluss getrennten Teile der Stadt sowie die Inseln waren, wie in der Abbildung ersichtlich, durch sieben Brücken miteinander verbunden. Die Einwohner der Stadt bewegte die Frage, ob es möglich wäre, die Stadt zu durchwandern und dabei alle Gebiete zu besuchen und dabei alle Brücken genau einmal zu überqueren. Jede Brücke müsste dabei vollständig überquert werden, d.h. es ist nicht erlaubt eine Brücke zunächst halb zu überqueren, dann zurückzukehren und später bei dem Rundgang die andere Hälfte zu begehen. Außerdem braucht die Wanderung nicht am gleichen Punkt zu beginnen und zu enden.
Leonard Euler löste das Problem im Jahre 1735, indem er bewies, dass es nicht lösbar ist. Er fand heraus, dass es irrelevant ist, welche Route man innerhalb eines zusammenhängenden Gebietes wählt, und dass es nur darauf ankommt, in welcher Reihenfolge die Brücken überquert werden. Er hatte damit ein Abstrakt des Problems formuliert, indem er unnötige Fakten eleminierte und sich auf die Landgebiete als Ganzes und die sie verbindenden Brücken konzentrierte. Damit schuf er die Grundlagen für die Graphentheorie. Wenn wir ein Landgebiet als Knoten und jede Brücke als eine Kante sehen, haben wir das Problem auf einen Graphen "reduziert".
Einführung in die Graphentheorie unter Python
Bevor wir unsere Abhandlung der Möglichen Darstellungen von Graphen in Python beginnen, wollen wir einige allgemeine
Definitionen von Graphen und deren Komponenten einführen.
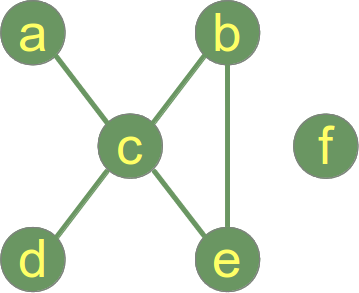
Ein "Graph"1 , in der Mathematik und der Informatik, besteht aus Knoten. Knoten können - müssen aber nicht - miteinander verbunden sein. In unserer Illustration, - eine bildliche Darstellung eines Graphen, - ist der Knoten "a" mit dem Knoten "c" verbunden, aber "a" ist nicht mit "b" verbunden. Die Verbindungslinie zwischen zwei Knoten nennt man ein Kante. Falls die Kanten zwischen den Knoten ungerichtet sind, wird der Graph als ungerichteter Graph bezeichnet. Falls die Kanten zwischen den Knoten gerichtet sind, spricht man von einem gerichteten Graphen.
Auch wenn Graphen sehr theoretisch erscheinen mögen, können viele praktische Sachverhalte und Probleme durch Graphen dargestellt werden. Sie werden oft benutzt, um Probleme oder Situationen der Informatik, der Physik, der Biologie, der Psychologie und anderer Wissenschaften zu modellieren.
Python hat keinen eingebauten (built-in) Datentyp oder Klasse für Graphen, aber es ist sehr einfach sie zu implementieren. Ein Datentyp eignet sich nahezu ideal um Graphen in Python zu realisieren: Dictionaries. Der Graph aus unserer Abbildung kann wie folgt in mit einem Dictionary codiert werden:
graph = { "a" : ["c"],
"b" : ["c", "e"],
"c" : ["a", "b", "d", "e"],
"d" : ["c"],
"e" : ["c", "b"],
"f" : []
}
Die Schlüssel des obigen Dictionaries entsprechen den Knoten unseres Graphen. Der korrespondierende Wert zu einem Schlüssel ist eine Liste mit den Knoten, die mit dem Knoten durch eine Kante verbunden sind. Es gibt wohl kaum eine einfachere und elegantere Möglichkeit einen Graphen zu codieren.
Eine Kante kann als 2-Tupel mit Knoten als Elementen gesehen werden, z.B. ("a","b")
Funktion zur Berechnung der Liste aller Kanten:
def generate_edges(graph):
edges = []
for node in graph:
for neighbour in graph[node]:
edges.append((node, neighbour))
return edges
print(generate_edges(graph))
Dieser Code erzeugt die folgende Ausgabe, wenn mann die Funktion auf dem vorher definierten Dictionary anwendet:
$ python3 graph_simple.py
[('a', 'c'), ('c', 'a'), ('c', 'b'), ('c', 'd'), ('c', 'e'), ('b', 'c'), ('b', 'e'), ('e', 'c'), ('e', 'b'), ('d', 'c')]
Wie wir sehen können, gibt es keine Kante, die den Knoten "f" enthält. "f" ist ein isolierter Knoten unseres Graphen.
Die folgende Python-Funktion ermittelt die isolierten Knoten eines Graphen:
def find_isolated_nodes(graph):
""" returns a list of isolated nodes. """
isolated = []
for node in graph:
if not graph[node]:
isolated += node
return isolated
Wenn wir diese Funktion mit unserem Graphen als Argument aufrufen, wird eine Liste mit dem Knoten "f" zurückgeliefert:
Graphen als Python-Klasse
Bevor wir weitere Funktionen für Graphen schreiben, wollen wir eine erste Implementierung für eine Graphklasse schreiben.
Schaut man sich das Listing unserer Klasse an, sieht man, dass wir in der __init__-Methode ein Dictionary "self.__graph_dict" zum Speichern der Knoten und ihrer benachbarten Knoten benutzen.
""" A Python Class
A simple Python graph class, demonstrating the essential
facts and functionalities of graphs.
"""
class Graph(object):
def __init__(self, graph_dict={}):
""" initializes a graph object """
self.__graph_dict = graph_dict
def vertices(self):
""" returns the vertices of a graph """
return list(self.__graph_dict.keys())
def edges(self):
""" returns the edges of a graph """
return self.__generate_edges()
def add_vertex(self, vertex):
""" If the vertex "vertex" is not in
self.__graph_dict, a key "vertex" with an empty
list as a value is added to the dictionary.
Otherwise nothing has to be done.
"""
if vertex not in self.__graph_dict:
self.__graph_dict[vertex] = []
def add_edge(self, edge):
""" assumes that edge is of type set, tuple or list;
between two vertices can be multiple edges!
"""
edge = set(edge)
(vertex1, vertex2) = tuple(edge)
if vertex1 in self.__graph_dict:
self.__graph_dict[vertex1].append(vertex2)
else:
self.__graph_dict[vertex1] = [vertex2]
def __generate_edges(self):
""" A static method generating the edges of the
graph "graph". Edges are represented as sets
with one (a loop back to the vertex) or two
vertices
"""
edges = []
for vertex in self.__graph_dict:
for neighbour in self.__graph_dict[vertex]:
if {neighbour, vertex} not in edges:
edges.append({vertex, neighbour})
return edges
def __str__(self):
res = "vertices: "
for k in self.__graph_dict:
res += str(k) + " "
res += "\nedges: "
for edge in self.__generate_edges():
res += str(edge) + " "
return res
if __name__ == "__main__":
g = { "a" : ["d"],
"b" : ["c"],
"c" : ["b", "c", "d", "e"],
"d" : ["a", "c"],
"e" : ["c"],
"f" : []
}
graph = Graph(g)
print("Vertices of graph:")
print(graph.vertices())
print("Edges of graph:")
print(graph.edges())
print("Add vertex:")
graph.add_vertex("z")
print("Vertices of graph:")
print(graph.vertices())
print("Add an edge:")
graph.add_edge({"a","z"})
print("Vertices of graph:")
print(graph.vertices())
print("Edges of graph:")
print(graph.edges())
print('Adding an edge {"x","y"} with new vertices:')
graph.add_edge({"x","y"})
print("Vertices of graph:")
print(graph.vertices())
print("Edges of graph:")
print(graph.edges())
Startet man diese Klasse als eigenständige (standalone) Applikation, erhält man folgende Ausgabe:
$ python3 graph.py
Vertices of graph:
['a', 'c', 'b', 'e', 'd', 'f']
Edges of graph:
[{'a', 'd'}, {'c', 'b'}, {'c'}, {'c', 'd'}, {'c', 'e'}]
Add vertex:
Vertices of graph:
['a', 'c', 'b', 'e', 'd', 'f', 'z']
Add an edge:
Vertices of graph:
['a', 'c', 'b', 'e', 'd', 'f', 'z']
Edges of graph:
[{'a', 'd'}, {'c', 'b'}, {'c'}, {'c', 'd'}, {'c', 'e'}, {'a', 'z'}]
Adding an edge {"x","y"} with new vertices:
Vertices of graph:
['a', 'c', 'b', 'e', 'd', 'f', 'y', 'z']
Edges of graph:
[{'a', 'd'}, {'c', 'b'}, {'c'}, {'c', 'd'}, {'c', 'e'}, {'a', 'z'}, {'y', 'x'}]
Pfade in Graphen
Wir wollen nun den kürzesten Pfad von einem Knoten zu einem anderen Knoten ermitteln. Bevor wir zum Python-Code für dieses Problem kommen, müssen wir noch ein paar formale Definitionen bringen:Benachbarte Knoten:
Zwei Knoten sind benachbart, wenn sie durch eine gemeinsame Kante verbunden sind.
Pfad in einem ungerichteten Graphen:
Ein Pfad in einem ungerichteten Graphen ist eine Folge von Knoten P = ( v1, v2, ..., vn ) ∈ V x V x ... x V so dass vi benachbart zu v{i+1} ist für alle 1 ≤ i < n. Ein solcher Pfad P wird als ein Pfad der Länge n von v1 nach vn bezeichnet.
Einfacher Pfad:
Ein Pfad ohne sich wiederholende Knoten wird als einfacher Pfad bezeichnet.
Beispiel:
Grad
Unter dem Grad (oft auch Knotengrad oder Valenz genannt) degG(v) eines Knotens v in einem Graphen versteht man die Anzahl der Kanten, die den Knoten v mit anderen Knoten verbinden. Eine Schlinge wird doppelt gezählt.
Der maximale Grad eines Graphen G wird mit Δ(G) bezeichnet und ist definiert als der maximale Grad der Knoten des Graphen. Der minimale Grad wird mit δ(G) bezeichnet und steht entsprechend für den minimalen Knotengrad.
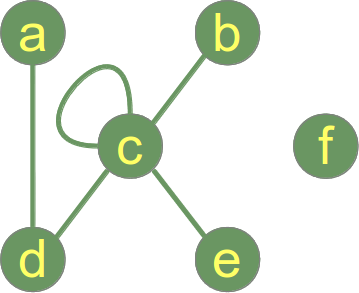
In dem Graphen der Abbildung auf der rechten Seite entspricht der maximale Grad dem Wert 5 am Knoten "c" und der minimale Grad dem Wert 0, da es sich bei "f" um einen isolierten Knoten handelt.
Falls alle Knotengrade in einem Graphen den gleichen Wert haben, wird dieser Graph als regulärer Graph bezeichnet. Da in einem regulären Graphen alle Grade gleich sind, können wir vom Grad eines Graphen sprechen. Anders ausgedrückt: Δ(G) = δ(G)
Handschlaglemma:
∑v ∈ Vdeg(v) = 2 |E|
Dies besagt, dass in jedem Graph die Summe der Grade über alle Knoten genau doppelt so groß ist wie die Anzahl seiner Kanten.
Daraus folgt unmittelbar, dass die Anzahl der Knoten eines Graphen mit ungeradem Grad gerade ist.
Für einen regulären Graph mit Grad k gilt die vereinfachte Formel:
k × |V| = |E|
Gradfolge
Unter der Gradfolge (auch Valenz- oder Gradsequenz genannt) eines einfachen Graphen versteht man eine nicht-aufsteigende Folge der Knotengrade der Knoten des Graphen.In unserem Beispiel lautet die Gradfolge (5,2,1, 1, 1,0).
Isomorphe Graphen haben die gleiche Gradfolge. Allerdings sind zwei Graphen mit gleicher Gradfolge nicht notwendigerweise isomorph.
Es stellt sich die Frage, ob es zu einer gegebenen Gradfolge auch einen einfachen Graph gibt. Der Satz von Erdös-Gallai besagt, dass jede nicht aufsteigende Folge von n natürlichen Zahlen di (für i = 1, ..., n) genau dann die Gradfolge eines einfachen Graphen darstellt, wenn die Summe der Folge gerade ist und darüber hinaus die folgende Bedingung erfüllt ist:
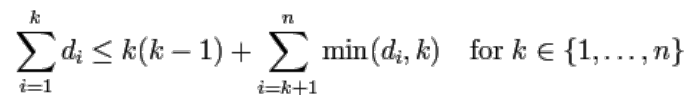
Implementierung des Satzes von Erdös-Gallai
Unsere Graphen-Klasse - ein komplettes Listing finden Sie weiter unten - enthält eine Methode "erdoes_gallai", die entscheidet, ob eine übergebene Folge die Bedingungen des Satzes von Erdös-Gallai erfüllt. Falls die Summe der Elemente der Folge ungerade ist, liefert die Funktion False zurück, weil damit der Satz von Erdös-Gallai nicht erfüllt ist. Die Methode benutzt dann die statische Methode is_degree_sequence, um sicherzustellen, dass die als Argument übergebene Folge auch wirklich eine Gradfolge ist, also dass die Elemente der Folge nicht aufsteigend sind. Daraufhin wird die Ungleichung des Satzes von Erdös-Gallai überprüft.
@staticmethod
def erdoes_gallai(dsequence):
""" Checks if the condition of the Erdoes-Gallai inequality
is fullfilled
"""
if sum(dsequence) % 2:
# sum of sequence is odd
return False
if Graph.is_degree_sequence(dsequence):
for k in range(1,len(dsequence) + 1):
left = sum(dsequence[:k])
right = k * (k-1) + sum([min(x,k) for x in dsequence[k:]])
if left > right:
return False
else:
# sequence is increasing
return False
return True
Version ohne den "überflüssigen" Gradfolgentest:
@staticmethod
def erdoes_gallai(dsequence):
""" Checks if the condition of the Erdoes-Gallai inequality
is fullfilled
dsequence has to be a valid degree sequence
"""
if sum(dsequence) % 2:
# sum of sequence is odd
return False
for k in range(1,len(dsequence) + 1):
left = sum(dsequence[:k])
right = k * (k-1) + sum([min(x,k) for x in dsequence[k:]])
if left > right:
return False
return True
Dichte eines Graphen
Unter der Dichte eines einfachen Graphen versteht man das Verhältnis von den real existierenden Kanten zu den potentiell möglichen Kanten. Die Dichte wird auch häufig als Kantendichte bezeichnet. Die Dichte eines Graphen ist 1, wenn es sich um einen vollständigen Graphen handelt. Dies ist klar, weil die maximale Anzahl der Kanten in einem Graphen von den Knoten abhängt und wie folgt berechnet werden kann:max. Kantenzahl = ½ * |V| * ( |V| - 1 ).
Für die Dichte eines Graphen ohne Kanten (isolierter Graph) ergibt sich ein Wert von 0. Dadurch folgt, dass die Werte für die Dichte beliebiger einfacher Graphen Werte zwischen 0 und 1 annehmen kann.
Die Dichte für ungerichtete einfache Graphen kann man damit wie folgt definieren:
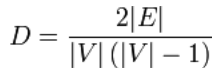
Ein dichter Graph ist ein Graph, in dem die Anzahl der Kanten nahe der maximal möglichen Kanten ist. Ein Graph mit nur wenigen Kanten wird als lichter Graph bezeichnet. Die beiden Begriffe sind nicht sehr scharf definiert, d.h. es gibt keine kleinste obere Schranke (Supremum) für die Dichte eines lichten Graphen und keine größte untere Schranke (Infimum) für einen dichten Graphen.
Etwas "genauer" kann man es mit der Landau-Notation (Groß-O) beschreiben:
Lichter Graph: Ein lichter Graph ist ein Graph G = (V, E) in dem gilt: |E| = O(|V|).
Dichter Graph: Ein dichter Graph ist ein Graph G = (V, E) in dem gilt: |E| = O(|V|).
"density" ist eine Methode unserer Graphklasse um die Dichte eines Graphen zu berechnen:
def density(self):
""" method to calculate the density of a graph """
g = self.__graph_dict
V = len(g.keys())
E = len(self.edges())
return 2.0 * E / (V *(V - 1))
Wir können die neue Methode mit folgendem Beispielprogramm testen:
from graph2 import Graph
g = { "a" : ["d","f"],
"b" : ["c","b"],
"c" : ["b", "c", "d", "e"],
"d" : ["a", "c"],
"e" : ["c"],
"f" : ["a"]
}
complete_graph = {
"a" : ["b","c"],
"b" : ["a","c"],
"c" : ["a","b"]
}
isolated_graph = {
"a" : [],
"b" : [],
"c" : []
}
graph = Graph(g)
print(graph.density())
graph = Graph(complete_graph)
print(graph.density())
graph = Graph(isolated_graph)
print(graph.density())
Wir können in den Ergebnissen des Beispielskriptes sehen, dass wir für einen vollständigen Graphen,
wie erwartet, den Wert 1 und für einen isolierten Graphen den Wert 0 erhalten:
$ python test_density.py 0.466666666667 1.0 0.0
Zusammenhangskomponente und zusammenhängender Graph
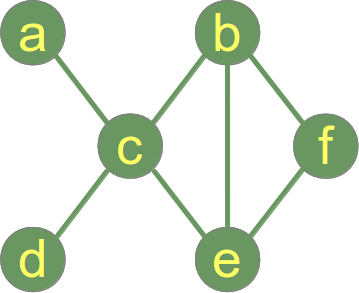Ein Graph G=(V,E) wird als zusammenhängend bezeichnet, falls es zu je zwei beliebigen Knoten v und w aus V einen Weg in G mit v als Startknoten und w als Endknoten gibt. Einen maximalen zusammenhängenden Teilgraphen von G nennt man eine Komponente oder Zusammenhangskomponente. Falls G nicht zusammenhängend ist zerfällt der Graph in seine Zusammenhangskomponenten. Der Beispielgraph auf der rechten Seite ist ein zusammenhängender Graph.
Man kann mit einem einfachen Algorthmus bestimmen, ob ein Graph zusammenhängend ist:
- Wähle einen beliebigen Knoten des Graphen G als Startpunkt.
- Bestimme die Menge A aller Knoten, die man von x aus erreichen kann.
- Falls A gleich der Menge der Knoten von G ist, ist der Graph zusammenhängend, ansonsten ist er nicht zusammenhängend.
Wir implementieren eine Methode is_connected, die prüft, ob ein Graph zusammenhängend ist. Bei der Implementierung geht es uns nicht um Effizienz sondern um Lesbarkeit.
def is_connected(self,
vertices_encountered = set(),
start_vertex=None):
""" determines if the graph is connected """
gdict = self.__graph_dict
vertices = gdict.keys()
if not start_vertex:
# chosse a vertex from graph as a starting point
start_vertex = vertices[0]
vertices_encountered.add(start_vertex)
if len(vertices_encountered) != len(vertices):
for vertex in gdict[start_vertex]:
if vertex not in vertices_encountered:
if self.is_connected(vertices_encountered, vertex):
return True
else:
return True
return False
Wenn wir diese Methode zu unserer Graphklasse hinzufügen, können wir sie mit dem folgenden Skript testen. Wir nehmen an, dass die Klasse unter dem Namen graph2.py gespeichert ist:
from graph2 import Graph
g = { "a" : ["d"],
"b" : ["c"],
"c" : ["b", "c", "d", "e"],
"d" : ["a", "c"],
"e" : ["c"],
"f" : []
}
g2 = { "a" : ["d","f"],
"b" : ["c"],
"c" : ["b", "c", "d", "e"],
"d" : ["a", "c"],
"e" : ["c"],
"f" : ["a"]
}
g3 = { "a" : ["d","f"],
"b" : ["c","b"],
"c" : ["b", "c", "d", "e"],
"d" : ["a", "c"],
"e" : ["c"],
"f" : ["a"]
}
graph = Graph(g)
print(graph)
print(graph.is_connected())
graph = Graph(g2)
print(graph)
print(graph.is_connected())
graph = Graph(g3)
print(graph)
print(graph.is_connected())
Eine Komponente oder eine Zusammenhangskomponente ist ein maximal zusammenhängender Untergraph von G. Jeder Knoten und jede Kante kann exakt einer Zusammenhangskomponente zugeordnet werden. Falls G nicht zusammenhängend ist zerfällt der Graph in seine Zusammenhangskomponenten.
Abstand und Durchmesser eines Graphen
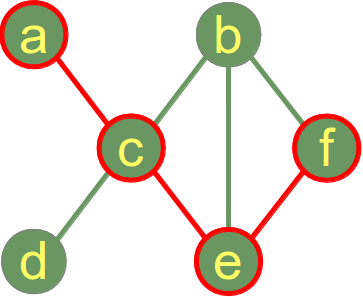Der Abstand "dist" zwischen zwei Kmoten in einem Graph ist die Länge des kürzesten Pfades zwischen diesen
Knoten. Keine Rückzieher, Umwege oder Schleifen sind bei der Berechnung des Abstandes erlaubt.
In unserem Beispielgraphen auf der rechten Seite entspricht der Abstand zwischen den Knoten a und f dem Wert 3, weil der kürzeste Weg über c und e (oder entsprechend über c und b) läuft, d.h. dist(a, f) = 3
Die Exzentrizität eines Knotens s ist der maximale Abstand zu allen anderen Knoten s des Graphen g:
e(s) = max( { dist(s,v) | v ∈ V })
Der Durchmesser d eines Graphen ist als die maximale Exzentrizität aller Knoten in dem Graphen definiert. Dies bedeutet, dass der Durchmesser dem kürzesten Pfad zwischen den am weitesten entferntesten Knoten entspricht.
Um den Durchmesser eines Graphen zu bestimmen, bestimmt man zuerst die kürzesten Pfade für alle Knotenpaare. Der längste dieser Pfade entspricht dem Durchmesser vom Graph.
Wir können unmittelbar in unserem Beispielgraph erkennen, dass der Durchmesser 3 ist, weil die minimale Länge zwischen a und f 3 ist und weil es keine anderen Knotenpaare mit einem längeren Weg gibt. Die folgende Methode "diameter" implementiert einen Algorithmus zur Berechnung des Durchmessers:
def diameter(self):
""" calculates the diameter of the graph """
v = self.vertices()
pairs = [ (v[i],v[j]) for i in range(len(v)-1) for j in range(i+1, len(v))]
smallest_paths = []
for (s,e) in pairs:
paths = self.find_all_paths(s,e)
smallest = sorted(paths, key=len)[0]
smallest_paths.append(smallest)
smallest_paths.sort(key=len)
# longest path is at the end of list,
# i.e. diameter corresponds to the length of this path
diameter = len(smallest_paths[-1])
return diameter
Wir können den Durchmesser unseres Beispielgraphen mit dem folgenden Programm berechnen:
from graph2 import Graph
g = { "a" : ["c"],
"b" : ["c","e","f"],
"c" : ["a","b","d","e"],
"d" : ["c"],
"e" : ["b","c","f"],
"f" : ["b","e"]
}
graph = Graph(g)
diameter = graph.diameter()
print(diameter)
Die Ausgabe ist 3.
Die komplette Graphklasse in Python
In dem folgenden Python-Code finden Sie das komplette Python-Klasse-Modul mit all den bisher besprochenen Methoden: graph2.pyBäume und Wälder
Ein Zyklus oder Kreis ist in der Graphentheorie ein Weg in einem Graphen, bei dem Start- und Endknoten gleich sind. Ein zyklischer Graph ist ein Graph mit mindestens einem Zyklus.Ein Baum ist ein ungerichteter Graph, der keine Zyklen enthält. Das bedeutet, dass zwei beliebige Knoten durch genau einen einfachen Pfad verbunden sind.
Ein Wald besteht aus einem oder mehreren Bäumen. Die stellen die Zusammenhangskomponenten eines Waldes dar.
Ein Graph mit einem Knoten und keiner Kante ist ein Baum und ein Wald.
Beispiel eines Baumes:
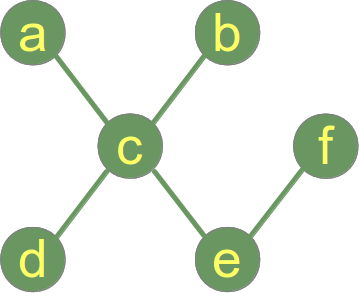
Während das vorige Beispiel einen Graphen darstellt, der sowohl ein Baum als auch ein Wald ist, sehen wir im Folgenden ein Beispiel für einen Graph, der ein Wald mit zwei Bäumen ist:
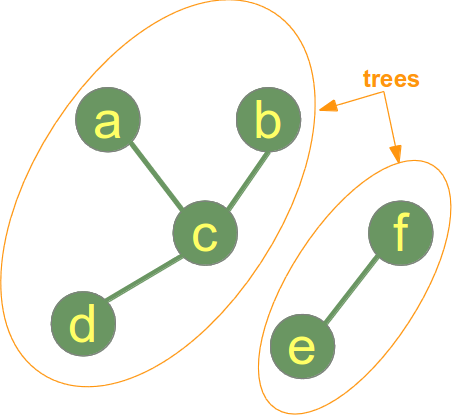
Übersicht über Wälder:
Wald mit einem Knoten:
Wälder mit zwei Knoten:
Wälder mit drei Knoten:
Spannbaum
Ein Spannbaum (auch aufspannender Baum) T eines ungerichteten Graphen G ist ein Untergraph G′, der ein Baum ist, alle Knoten von G und eine Untermenge der Kanten enthält. Falls G′ alle Kanten von G enthält, dann ist G′ ein Baumgraph.Beispiel:
Ein vollständiger Graph:
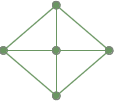
Zwei Spannbäume des vorigen vollständigen Graphen:
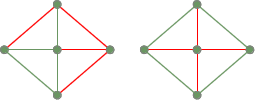
Hamiltonkreisproblem
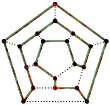
Der Name des Problems geht auf den irischen Astronom und Mathematiker Sir William Rowan Hamilton zurück, der 1857 das Spiel "The Icosian Game" erfand. Später wurde es in "Traveller's Dodecahedron or A Voyage Round The World" verbessert.
Ein Graph G = (V,E) ist hamiltonsch, wenn er einen Hamiltonkreis zulässt, d.h., wenn es einen Kreis in G gibt, der alle Knoten aus V enthält. Ein Hamiltonpfad ist ein Pfad in G, der alle Knoten aus V enthält. Hat G Hamiltonpfade, jedoch keinen Hamiltonkreis, so ist G semihamiltonsch.
Für Informatiker: Im Allgemeinen ist es nicht möglich zu entscheiden, ob Pfade oder Zyklen in einem beliebigen Graph existieren, weil das Hamiltonsche Pfadproblem NP-vollständig ist.
Vollständiges Listing der Pfadklasse
""" A Python Class
A simple Python graph class, demonstrating the essential
facts and functionalities of graphs.
"""
class Graph(object):
def __init__(self, graph_dict={}):
""" initializes a graph object """
self.__graph_dict = graph_dict
def vertices(self):
""" returns the vertices of a graph """
return list(self.__graph_dict.keys())
def edges(self):
""" returns the edges of a graph """
return self.__generate_edges()
def add_vertex(self, vertex):
""" If the vertex "vertex" is not in
self.__graph_dict, a key "vertex" with an empty
list as a value is added to the dictionary.
Otherwise nothing has to be done.
"""
if vertex not in self.__graph_dict:
self.__graph_dict[vertex] = []
def add_edge(self, edge):
""" assumes that edge is of type set, tuple or list;
between two vertices can be multiple edges!
"""
edge = set(edge)
vertex1 = edge.pop()
if edge:
# not a loop
vertex2 = edge.pop()
else:
# a loop
vertex2 = vertex1
if vertex1 in self.__graph_dict:
self.__graph_dict[vertex1].append(vertex2)
else:
self.__graph_dict[vertex1] = [vertex2]
def __generate_edges(self):
""" A static method generating the edges of the
graph "graph". Edges are represented as sets
with one (a loop back to the vertex) or two
vertices
"""
edges = []
for vertex in self.__graph_dict:
for neighbour in self.__graph_dict[vertex]:
if {neighbour, vertex} not in edges:
edges.append({vertex, neighbour})
return edges
def __str__(self):
res = "vertices: "
for k in self.__graph_dict:
res += str(k) + " "
res += "\nedges: "
for edge in self.__generate_edges():
res += str(edge) + " "
return res
def find_isolated_vertices(self):
""" returns a list of isolated vertices. """
graph = self.__graph_dict
isolated = []
for vertex in graph:
print(isolated, vertex)
if not graph[vertex]:
isolated += [vertex]
return isolated
def find_path(self, start_vertex, end_vertex, path=[]):
""" find a path from start_vertex to end_vertex
in graph """
graph = self.__graph_dict
path = path + [start_vertex]
if start_vertex == end_vertex:
return path
if start_vertex not in graph:
return None
for vertex in graph[start_vertex]:
if vertex not in path:
extended_path = self.find_path(vertex,
end_vertex,
path)
if extended_path:
return extended_path
return None
def find_all_paths(self, start_vertex, end_vertex, path=[]):
""" find all paths from start_vertex to
end_vertex in graph """
graph = self.__graph_dict
path = path + [start_vertex]
if start_vertex == end_vertex:
return [path]
if start_vertex not in graph:
return []
paths = []
for vertex in graph[start_vertex]:
if vertex not in path:
extended_paths = self.find_all_paths(vertex,
end_vertex,
path)
for p in extended_paths:
paths.append(p)
return paths
def is_connected(self,
vertices_encountered = set(),
start_vertex=None):
""" determines if the graph is connected """
gdict = self.__graph_dict
vertices = gdict.keys()
if not start_vertex:
# chosse a vertex from graph as a starting point
start_vertex = vertices[0]
vertices_encountered.add(start_vertex)
if len(vertices_encountered) != len(vertices):
for vertex in gdict[start_vertex]:
if vertex not in vertices_encountered:
if self.is_connected(vertices_encountered, vertex):
return True
else:
return True
return False
def vertex_degree(self, vertex):
""" The degree of a vertex is the number of edges connecting
it, i.e. the number of adjacent vertices. Loops are counted
double, i.e. every occurence of vertex in the list
of adjacent vertices. """
adj_vertices = self.__graph_dict[vertex]
degree = len(adj_vertices) + adj_vertices.count(vertex)
return degree
def degree_sequence(self):
""" calculates the degree sequence """
seq = []
for vertex in self.__graph_dict:
seq.append(self.vertex_degree(vertex))
seq.sort(reverse=True)
return tuple(seq)
@staticmethod
def is_degree_sequence(sequence):
""" Method returns True, if the sequence "sequence" is a
degree sequence, i.e. a non-increasing sequence.
Otherwise False is returned.
"""
# check if the sequence sequence is non-increasing:
return all( x>=y for x, y in zip(sequence, sequence[1:]))
def delta(self):
""" the minimum degree of the vertices """
min = 100000000
for vertex in self.__graph_dict:
vertex_degree = self.vertex_degree(vertex)
if vertex_degree < min:
min = vertex_degree
return min
def Delta(self):
""" the maximum degree of the vertices """
max = 0
for vertex in self.__graph_dict:
vertex_degree = self.vertex_degree(vertex)
if vertex_degree > max:
max = vertex_degree
return max
def density(self):
""" method to calculate the density of a graph """
g = self.__graph_dict
V = len(g.keys())
E = len(self.edges())
return 2.0 * E / (V *(V - 1))
def diameter(self):
""" calculates the diameter of the graph """
v = self.vertices()
pairs = [ (v[i],v[j]) for i in range(len(v)) for j in range(i+1, len(v)-1)]
smallest_paths = []
for (s,e) in pairs:
paths = self.find_all_paths(s,e)
smallest = sorted(paths, key=len)[0]
smallest_paths.append(smallest)
smallest_paths.sort(key=len)
# longest path is at the end of list,
# i.e. diameter corresponds to the length of this path
diameter = len(smallest_paths[-1])
return diameter
@staticmethod
def erdoes_gallai(dsequence):
""" Checks if the condition of the Erdoes-Gallai inequality
is fullfilled
"""
if sum(dsequence) % 2:
# sum of sequence is odd
return False
if Graph.is_degree_sequence(dsequence):
for k in range(1,len(dsequence) + 1):
left = sum(dsequence[:k])
right = k * (k-1) + sum([min(x,k) for x in dsequence[k:]])
if left > right:
return False
else:
# sequence is increasing
return False
return True
Fußnoten:
1 Die Graphen der Graphentheorie (und die in diesem Tutorial behandelten, sollten nicht mit den Graphen von Funktionen verwechselt werden.