Türme von Hanoi


Einführung

Warum präsentieren wir in den weiterführenden Themen eine rekursive Python-Implementierung des mathematischen Knobelspiels "Türme von Hanoi"? Wir finden, dass es ein weiteres tolles Beispiel ist, an dem man sehen kann, wie elegant sich auch scheinbar schwierige Probleme mittels Rekursion lösen lassen. Sollte jemand mit der rekursiven Programmierung und rekursiven Funktionen noch nicht vertraut sein, so empfehlen wir unser Kapitel "Rekursive Funktionen", in dem man die Standard-Beispiel wie die Fakultätsfunktion und eine rekusive Berechnung der Fibonacci-Zahlen findet. Funktionen ganz allgemein behandeln wir in "Funktionen".

Die üblichen Beispiele für Rekursion, also Fibonacci und Fakultät, zeichnen sich dadurch aus, dass man auch relativ leicht eine iterative Lösung bestimmen kann. Anders sieht es mit den Türmen von Hanoi an. Eine rekursive Lösung ist deutlich leichter zu finden als eine iterative, obwohl es natürlich auch hierzu eine iterative Lösung gibt.

Ursprung

Towers of Hanoi
Eine alte Legende berichtet von einem Kloster oder einem Tempel irgenwo in China oder Indien, in dem es drei Stäbe gibt, von denen einer mit 64 Goldscheiben besetzt ist. Die Scheiben haben verschiedene Größen und sind der Größe nach übereinander gestapelt, d.h. jede Scheibe ist etwas kleiner als die darunter liegende. Die Mönche oder Priester haben die Aufgabe diesen Stapel von einem Stab auf einen anderen Stab zu bewegen.

Aber eine Regel muss immer eingehalten werden: eine Scheibe darf unter keinen Umständen auf einer kleineren Scheibe platziert werden. Aber man sollte den Möchen keinesfalls die Daumen drücken, dass sie möglichst bald fertig werden. Denn die Legende sagt, dass das Kloster zu Staub zerfallen und die Welt enden wird, sobald sie ihre Aufgabe erfüllt haben werden.

Aber es besteht kein Grund für Panik oder Angst, denn es ist nicht sehr wahrscheinlich, dass sie es schaffen, denn es sind dazu 264 - 1 Züge nötig, also 18,446,744,073,709,551,615 Züge.


Spielregeln

Obwohl die Regeln dieses Spieles recht einfach sind, ist die Lösung nicht so einfach zu finden.

Das Spiel benutzt drei Stäbe und eine Anzahl von Scheiben z.B. 9, die auf die Stäbe gesteckt werden können. Anfänglich befinden sich alle Scheiben in absteigender Größe auf einem Stab angeordnet, d.h. die größte ist ganz unten und die kleinste ganz oben. Die Scheiben auf diesem Stab bilden einen konischen Turm. Die Aufgabe besteht darin, diesen Turm von einem Stab auf einen anderen zu bewegen unter Beachtung der folgenden Regeln:

Anzahl der Züge

Die minimal notwendige Anzahl von Zügen, die notwendig sind, um einen Turm der Größe n von einem Stab auf einen anderen unter Einhaltung der Regeln zu bewegen, lässt sich wie folgt berechnen: 2n - 1

Lösungsfindung


Nach der obigen Formel wissen wir, dass wir 7 Züge benötigen, um einen Turm der Größe 3 von dem ganz linken Stab, den wir im folgenden SOURCE nennen werden, auf den Stab ganz rechts, den wir TARGET nennen werden, zu bewegen.

Der mittlere Stab, den wir mit AUX bezeichnen, wird als Hilfsstab benötigt, um Scheiben temporär zwischenzulagern.

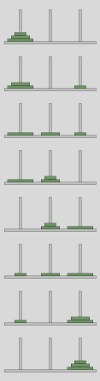Towers of Hanoi Bevor wir uns mit dem 3-Scheiben-Fall beschäftigen, so wie er im Bild auf der rechten Seite dargestellt ist, schauen wir uns noch Türme der Größe 1 (also nur eine Scheibe) und 2 an.

Ein Turm mit nur einer Scheibe lässt sich in trivialer Weise verschieben. Man nimmt die Scheibe vom Stab SOURCE und bewegt sie auf den Stab TARGET.

Schauen wir uns nun einen Turm der Größe 2 an, also zwei Scheiben. Es gibt nur zwei Möglichkeiten die erste Scheibe, also die oberste Scheibe auf dem Stapel SOURCE, zu verschieben. Wir können sie entweder auf TARGET oder auf AUX bewegen. In den Fällen n=1 und n=2 haben wir gesehen, dass es auf den ersten Zug ankommt, ob wir erfolgreich mit der minimalen Anzahl von Zügen das Rätsel lösen können. Mit unserer Formel können wir die minimale Anzahl von Zügen berechnen, die notwendig ist einen Turm mit 3 Scheiben von SOURCE Stab auf den TARGET Stab zu verschieben: 7 ( entspricht 23 - 1).
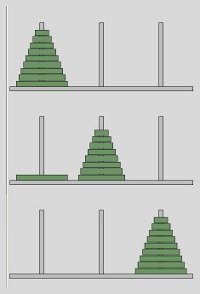
In dem Bild auf der rechten Seite kann man die Lösung für den Fall n = 3 sehen. Man beginnt also mit dem Zug, dass man die oberste Scheibe von SOURCE auf TARGET bewegt. Startet man dagegen mit dem Zug TARGET nach AUX, wird man nicht mehr in der Lage sein, die Aufgabe in weniger als 9 Zügen zu bewerkstelligen. 7 Züge ist aber das Ziel. Towers of Hanoi, n disks

Nummerieren wir die Scheiben mit D1 (kleinste), D2 and D3 (größte) und bezeichnen wir die Stäbe mit S (SOURCE), A (AUX) und T (TARGET). Wir erkennen, dass wir in drei Zügen den Turm der Größe 2, d.h. die Scheiben D1 und D2 nach A bewegen. Nun können wir die Scheibe D3 nach T bewegen, wo sie endgültig positioniert bleibt. In den nächsten drei Zügen bewegen wir den Turm von A, bestehend aus den Scheiben D2D1 von A nach T auf die Scheibe D3.

Nun überlegen wir uns das Vorgehen zum Verschieben von Türme beliebiger Größe n von Stab S nach Stab T: Der Algorithmus, den wir gerade definiert haben, ist ein rekursiver Algorithmus um Türme mit n Scheiben zu verschieben. Wir werden diesen Algorithmus in Python als rekursive Funktion implementieren. Der zweite Schritt ist eine einfache Bewegung einer Scheibe, aber um die Schritte 1 und 3 zu verwirklichen, müssen wir den Algorithmus wieder auf sich selbst anwenden. Die Berechnung endet in einer endlichen Anzahl von Schritten, da die Rekursion jedesmal mit einem um 1 verminderten Argument gegenüber der aufrufenden Funktion gestartet wird. Am Schluss ist noch eine einzelne zu bewegende Scheibe übrig.

Rekursives Python-Programm

Das folgende in Python geschriebene Skript enthält eine rekursive Funktion namens "hanoi" zur Lösung des Spiels "Türme von Hanoi": 
def hanoi(n, source, helper, target):
    if n > 0:
        # move tower of size n - 1 to helper:
        hanoi(n - 1, source, target, helper)
        # move disk from source peg to target peg
        if source:
            target.append(source.pop())
        # move tower of size n-1 from helper to target
        hanoi(n - 1, helper, source, target)
        
source = [4,3,2,1]
target = []
helper = []
hanoi(len(source),source,helper,target)

print source, helper, target
Anmerkung: AUX heißt in unserem Programm "helper".

Wir haben diese Funktion analog zum im vorigen Unterkapitel geschriebenen implementiert. Wir bewegen also zuerst einen Turm der Größe n-1 von "source" auf "helper". Dies geschieht durch den Aufruf 
hanoi(n - 1, source, target, helper)

Danach bewegen wir die größte Scheibe von "source" auf "target mit der folgenden Anweisung: 
        if source:
            target.append(source.pop())
Danach bewegen wir den Turm von "helper" nach "target", d.h. wir setzen ihn auf die größte Scheibe und sind dann fertig: 
        hanoi(n - 1, helper, source, target)
Wenn man nachvollziehen will, was während des Ablaufs passiert, so empfehlen wir die folgende geänderte Version unseres Python-Programmes zu verwenden. Wir haben nicht nur ein paar prints eingebaut sondern auch die Datenstruktur geringfügig geändert. Wir übergeben jetzt nicht nur die Stäbe mit Scheiben sondern Tuple an die Funktion. Jedes Tuple enthält zum einen den Stab mit seinem Inhalt und als zweite Komponente, die Funktion des Stabes: 
def hanoi(n, source, helper, target):
    print "hanoi( ", n, source, helper, target, " called"
    if n > 0:
        # move tower of size n - 1 to helper:
        hanoi(n - 1, source, target, helper)
        # move disk from source peg to target peg
        if source[0]:
            disk = source[0].pop()
            print "moving " + str(disk) + " from " + source[1] + " to " + target[1]
            target[0].append(disk)
        # move tower of size n-1 from helper to target
        hanoi(n - 1, helper, source, target)
        
source = ([4,3,2,1], "source")
target = ([], "target")
helper = ([], "helper")
hanoi(len(source[0]),source,helper,target)

print source, helper, target