for-Schleifen

Syntax der For-Schleife

Ring als Symbol der for-Schleife

for Variable in Sequenz:
	Anweisung1
	Anweisung2
	...
	Anweisungn
else:
	Else-Anweisung1
	Else-Anweisung2
	...
	Else-Anweisungm
Die for-Anweisung hat einen unterschiedlichen Charakter zu den for-Schleifen, die man aus den meisten anderen Programmiersprachen kennt. In Python dient die for-Schleife zur Iteration über ein Sequenz von Objekten, während sie in anderen Sprachen meist nur "eine etwas andere while-Schleife" ist.
Beispiel einer for-Schleife in Python: 
>>> languages = ["C", "C++", "Perl", "Python"] 
>>> for x in languages:
...     print x
... 
C
C++
Perl
Python
>>>

Die range()-Funktion

Mit Hilfe der range()-Funktion lässt sich die for-Schleife ideal für Iterationen nutzen. range() liefert Listen, die arithmetischen Aufzählungen entsprechen.
Beispiel: 

>>> range(10)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Obiges Beispiel zeigt, dass Range mit einem Argument aufgerufen die Liste der Zahlen von 0 bis zu diesem Argument liefert.
range() kann aber auch mit zwei Argumenten aufgerufen werden: 
range(begin,end)
Dann wird eine Liste aller ganzen Zahlen von begin (einschließlich) bis end (aussschließlich) geliefert.
Als drittes Argument kann man range() noch die Schrittweite mitgeben.
Beispiel: 
>>> range(4,10)
[4, 5, 6, 7, 8, 9]
>>> range(4,50,5)
[4, 9, 14, 19, 24, 29, 34, 39, 44, 49]
Besonders sinnvoll wird die range()-Funktion im Zusammenspiel mit der for-Schleife. Im nachfolgenden Beispiel bilden wir die Summe der Zahlen von 1 bis 100: 
n = 100
s = 0
for i in range(1, n+1):
    s = s + i
print s

In obigem kleinen Programm verbirgt sich aber noch ein schreckliches Effizienzproblem. Was geschieht bevor die for-Schleife ausgeführt wird? Python wertet zuerst den Aufruf range(1, n+1) aus. Das bedeutet, dass eine Liste mit 100 Zahlen erzeugt wird, also [1, 2, 3, 4, ... 100]. Es werden zwar alle Zahlen dieser Liste innerhalb der Schleife benötigt, aber zu keinem Zeitpunkt die ganze Liste. Im vorigen Kapitel hatte wir dieses Problem mit einer while-Schleife gelöst und dort benötigten wir auch keine Liste. Python bietet eine Lösung für dieses Problem, indem es die Funktion xrange zur Verfügung stellt. xrange erzeugt ein iterierbares Objekt (iterable), das bedeutet, dass keine Liste erzeugt wird sondern zum Beispiel in einer for-Schleife über die Werte iteriert werden kann ohne dass die Liste erzeugt wird: 
>>> for i in xrange(1, 7):
...     print(i)
... 
1
2
3
4
5
6
>>>
Obige Schleife verhält sich im Hinblick auf die Effizienz ähnlich wie folgende while-Schleife: 
>>> i = 1
>>> while i < 7:
...     print(i)
...     i  += 1
... 
1
2
3
4
5
6
>>>
Im Ausgabeverhalten sieht man natürlich keinen Unterschied. Den Unterschied zwischen range und xrange sieht man aber, wenn man die Aufrufe direkt in der interaktiven Python-Shell tätigt: 
>>> range(1,7)
[1, 2, 3, 4, 5, 6]
>>> xrange(1,7)
xrange(1, 7)
>>>


Beispiel: Berechnung der pythagoräischen Zahlen

Beweis des Satzes von Pythagoras Die meisten glauben, dass der Satz von Pythagoras von Pythagoras entdeckt worden war. Warum sonst sollte der Satz seinen Namen erhalten haben. Aber es gibt eine Debatte, ob dieser Satz nicht auch unabhängig von Pyhtagoras und vor allen Dingen bereits früher entdeckt worden sein könnte. Für die Pythagoräer - eine mystische Bewegung, die sich auf die Mathematik, Religion und die Philosophie begründete - waren die ganzen Zahlen, die den Satz des Pythagoras erfüllten besondere Zahlen, die für sie heilig waren.

Heutzutage haben die Pythagoräischen Zahlen nichts mystisches mehr. Obwohl sie für manche Schülerin oder Schüler oder ander Personen, die mit der Mathematik auf Kriegsfuß stehen, immer noch so erscheinen mögen.
Ganz unromantisch gilt in der Mathematik:
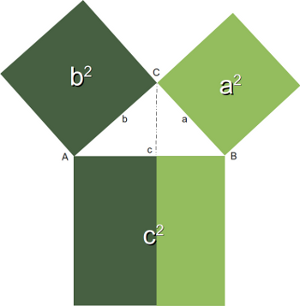
Drei natürliche Zahlen, welche die Gleichung a2+b2=c2 erfüllen, heißen pythagoräische Zahlen.
Das folgende Programm berechnet alle pythagoräischen Zahlen bis zu einer einzugebenden maximalen Zahl: 
#!/usr/bin/env python
from math import sqrt
n = raw_input("Maximale Zahl? ")
n = int(n)+1
for a in xrange(1, n):
    for b in xrange(a, n):
        c_square = a**2 + b**2
        c = int(sqrt(c_square))
        if ((c_square - c**2) == 0):
            print a, b, c

Iteration über Liste mit range()

Falls man auf die Indexe einer Liste zugreifen möchte, scheint es keine gute Idee zu sein eine For-Schleife zur Iteration über die Liste zu nutzen. Man kann dann zwar alle Elemente erreichen, aber der Index eines Elementes ist nicht verfügbar. Aber es gibt eine Möglichkeit sowohl auf den Index als auch auf das Element zugreifen zu können. Die Lösung besteht darin range() in Kombination mit der len()-Funktion, die einem die Anzahl der Listenelemente liefert, zu benutzen: 
fibonacci = [0,1,1,2,3,5,8,13,21]
for i in xrange(len(fibonacci)):
    print i,fibonacci[i]
print

Listen-Iteration mit Seiteneffekten

Falls man über eine Liste iteriert, sollte man vermeiden die Liste im Schleifenkörper (body) zu verändern. Was passieren kann, zeigen wir im folgenden Beispiel: 
colours = ["red"]
for i in colours:
    if i == "red":
        colours += ["black"]
    if i == "black":
        colours += ["white"]
print colours
Was wird durch die Anweisung "print colours" ausgegeben? 
['red', 'black', 'white']
Am besten benutzt man eine Kopie der Liste, wie im nächsten Beispiel: 
colours = ["red"]
for i in colours[:]:
    if i == "red":
        colours += ["black"]
    if i == "black":
        colours += ["white"]
print colours
Die Ausgabe sieht nun wie folgt aus: 
['red', 'black']
Auch jetzt haben wir die Liste verändert, aber "bewusst" innerhalb des Schleifenkörpers. Aber der Elemente, die über die For-Schleife interiert werden, bleiben unverändert durch die Iterationen.