Memoisation und Dekorateure
Definition der Memoisation
Der Ausdruck "Memoisation" (englisch memoization) wurde im Jahre 1968 von Donald Michie geprägt. Der Ausdruck basiert auf dem lateinischen Wort "memorandum", was "das zu Erinnernde" bedeutet. Memoisation bezeichnet in der Informatik eine Technik, die in der Programmierung benutzt wird, um den Programmablauf zu beschleunigen. Dies wird erreicht, indem Berechnungsergebnisse gespeichert werden, wie zum Beispiel die Ergebnisse von Funktionsaufrufen. Wird eine Funktion mit den gleichen Parametern aufgerufen, wie bei einem vorigen Aufruf, wird auf die gespeicherten Ergebnisse zugegriffen statt die Werte neu zu berechnen. In vielen Fällen wird ein einfaches Array für die Ergebnisspeicherung benutzt, aber es sind auch kompliziertere Strukturen möglich. So können beispielsweise assoziative Arrays verwendet werden, die in Perl Hashes und in Python Dictionaries genannt werden.
Die Memoization kann explizit vom Programmierer programmiert werden, aber einige Programmiersprachen, wie auch Python, stellen Mechanismen zur Verfügung, die die Implementierung der Memoisation erleichtern.
Memoisation mit Dekorateur-Funktionen
In unserem vorigen Kapitel über rekursive Funktionen hatten wir eine iterative und eine rekursive Funktionsversion zur Berechnung der Fibonacci-Zahlen programmiert. Wir hatten gezeigt, dass die direkte Umsetzung der mathematischen Definition der Fibonacci Zahlen ein exponentielles Laufzeitverhalten aufzeigt, also eine Funktion wie die folgende:
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
In unserem Kapitel über Rekursion hatten wir auch einen Weg dargestellt, wie man das Laufzeitverhalten der rekursiven Version verbessern kann. Wir hatten ein Dictionary dazu verwendet, um bereits durch die Funktion berechnete Werte für spätere Aufrufe zu speichern. Dadurch wird eine Neuberechnung verhindert. Dabei handelte es sich bereits, ohne dass wir es so genannt hatten, um ein Beispiel, wie man explizit die Technik der Memoization nutzen kann. Die Methode hatte jedoch einen entscheidenden Nachteil: Die Klarheit und die Schönheit der ursprünglichen rekursiven Methode geht dabei verloren.
Das "Problem" besteht darin, dass wir den Code der rekursiven fib-Funktion ändern bzw. erweitern mussten. Im folgenden Code präsentieren wir eine Lösung, die ohne Änderungen der fib-Funktion auskommt. Dadurch wird ihre Klarheit, Schönheit und Lesbarkeit nicht tangiert. Zu diesem Zweck definieren wir eine Funktion, die wir memoize nennen. memoize() benötigt zwei Argumente. Auch die Funktion memoize benutzt ein Dictionary, um die Funktionswerte zu speichern. Obwohl sowohl die Variable "memo", - unser Dictionary zum Speichern der Werte, - als auch die Funktion "f" lokal innerhalb der Funktion memoize sind, werden ihre Werte durch die helper-Funktion bewahrt. Im Englischen benutzt man statt "bewahrt" das Wort "captured", was im Deutschen "eingefangen" oder "gefangen genommen" bedeutet. Diese Technik, d.h. das Bewahren von ,,lokalen'' Werten oder Funktionen über ihren lokalen Geltungsbereich hinaus wird auch als Closure oder Funktionsabschluss bezeichnet. memoize() liefert als Funktionswert eine Referenz auf die helper-Funktion zurück. Ein Aufruf der Funktion memoize(fib) liefert eine Funktion zurück, die im Ein- und Ausgabeverhalten identisch mit fib() ist, d.h. sie tut, was fib() tut. Zusätzlich speichert sie jedoch die Ergebnisse im memo-Dictionary.
def memoize(f):
memo = {}
def helper(x):
if x not in memo:
memo[x] = f(x)
return memo[x]
return helper
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
fib = memoize(fib)
print(fib(40))
Als nächstem Punkt kommen wir zu einem Konzept, was als "Dekorateur" (englisch decorator: Raumgestalter, Dekorateur) bezeichnet wird. Schauen wir uns die folgende Codezeile an:
fib = memoize(fib)
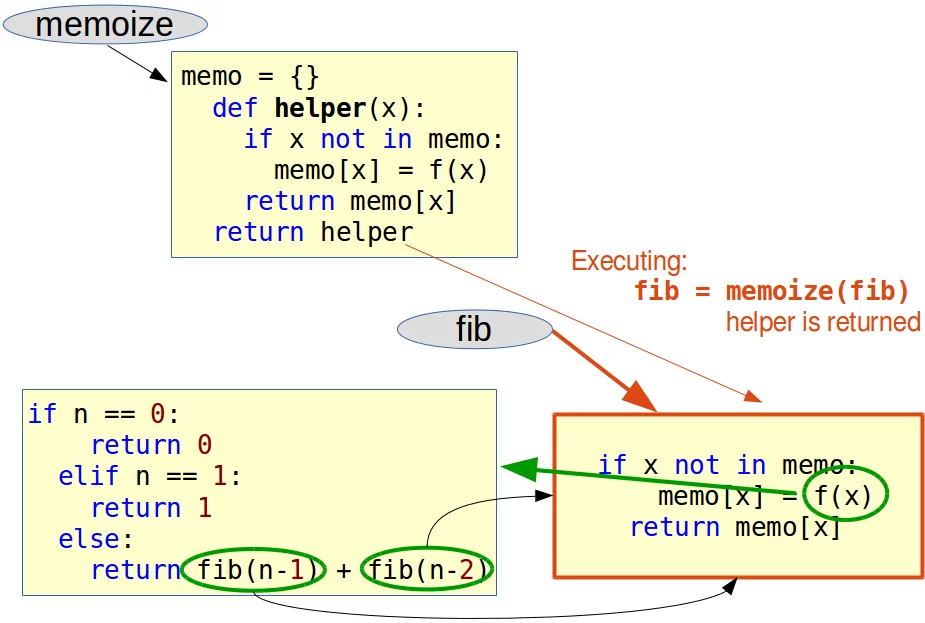
In diesem Fall spricht man davon, dass die fib-Funktion durch die memoize-Funktion dekoriert wird. In den folgenden Diagrammen verdeutlichen wir, was bei der Dekoration passiert. Im ersten Diagramm zeigen wir den Zustand der Funktionen vor der Dekoration. Wir sehen die Namen der Funktionen mit Referenzen auf ihre Funktionsbodies:

Nach dem Ausführen der Zeile fib = memoize(fib) zeigt fib auf den Body der Helper-Funktion, der nach dem Aufruf memoize(fib) zurückgeliefert wird. Wir können außerdem erkennen, dass der Code der ursprünglichen Fib-Funktion nur noch durch f in der Helper-Funktion aufgerufen wird bzw. aufgerufen werden kann. Es gibt sonst keine Referenz mehr auf die ursprüngliche fib-Funktion. Im return-Statement return fib(n-1) + fib(n-2) wird nun die neue, dekorierte Fibonacci-Funktion aufgerufen, d.h. die von memoize zurückgelieferte helper-Funktion:
Ein weiterer Punkt im Zusammenhang mit Dekorateuren verdient auch besondere Erwähnung. In der Regel schreiben wir einen Dekorator nicht für einen speziellen Anwendungsfall sondern verwenden den Dekorator für viele Funktionen. So könnten wir beispielsweise weitere Funktionen haben, die alle viel Zeit für die Berechnung konsumieren, sagen wir func1, func2, func3 und so weiter. Es bietet sich dann an, alle mit unserer Dekoratorfunktion "memoize" zu dekorieren:
fib = memoize(fib) func1 = memoize(func1) func2 = memoize(func2) func3 = memoize(func3) # und so weiter
Memoize in einer Klasse
Dieses Unterkapitel kann von denen problemlos übersprungen werden, die sich noch nicht mit der Objektorientierung in Python beschäftigt haben.
Wir können das Zwischenspeichern der Ergebnisse auch in einer Klasse statt einer Funktion einkapseln. Wir demonstrieren dies im folgenden kleinen Beispiel:
class Memoize:
def __init__(self, fn):
self.fn = fn
self.memo = {}
def __call__(self, *args):
if args not in self.memo:
self.memo[args] = self.fn(*args)
return self.memo[args]
Da wir ein Dictionary verwenden, können wir keine veränderlichen (mutable) Argumente verwenden. Anders ausgedrückt: Die Argumente dürfen nur unveränderlich (immutable), also z.B. Tupel, sein.
Übliche Syntax für Dekorateure
Zusammenfassend können wir nun sagen, dass ein Dekorateur in Python ein aufrufbares Python-Objekt ist, welches benutzt wird, um eine Funktion, eine Methode oder eine Klassendefinition zu modifizieren. Das ursprüngliche Objekt, also das zu modifizierende, wird dem Dekorateur als Argument zugeführt. Der Dekorateur liefert ein modifiziertes Objekt zurück, also beispielsweise eine modifizierte Funktion. Dieses modifizierte Objekt wird an den Namen gebunden, der modifiziert wird.
Anders als in unserem obigen Beispiel werden die Dekoratorfunktionen nicht direkt aufgerufen, wie wir es oben getan haben, also in unserem Beispiel mit fib = memoize(fib). Stattdessen stellt man vor den Funktionsheader der zu dekorierenden Funktion eine Zeile mit dem Dekoratornamen. Dem Dekoratornamen wird aber ein "@" vorangestellt. Diese Zeile muss unmittelbar vor der zu dekorierenden Funktion stehen.
Wir schreiben nun unser anfängliches Beispiel entsprechend um. Wir dekorieren unsere fib-Funktion mit @memoize. Damit sieht unser Fibonacci-Beispiel wie folgt aus:
def memoize(f):
memo = {}
def helper(x):
if x not in memo:
memo[x] = f(x)
return memo[x]
return helper
@memoize
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
print(fib(40))
Memoisation mit functools.lru_cache
Das Modul functools enthält einen komfortablen Dekorateur zur Memoisation und zwar den lru_cache-Dekorateur. Die Buchstaben "lru" stehen für "least recently used" (am längsten nicht verwendet), das bedeutet, dass sich der Dekorator nur die zuletzt berechneten Werte in einem limitierten Cache merkt.
import functools
@functools.lru_cache()
def fib(n):
if n < 2:
return n
else:
return fib(n-1) + fib(n-2)
Die Arbeitsweise dieses Dekorateurs können wir am Besten aus folgendem Beispiel ersehen:
import functools
@functools.lru_cache()
def f(x):
return x
f.cache_info()
f(1)
f(3)
f(1)
f.cache_info()
f.cache_info() liefert die Cache-Statistik (hits, misses, maxsize, currsize) zurück. f.cache_clear() löscht den Cache und die Statistik. Bei dem lru_cach-Dekorateur handelt es sich um einen Dekorateur, der mit Parametern aufgerufen wird. Er kann mit den beiden Schlüsselwort-Paramet aufgerufen werden. In unserem Beispielaufruf wurden für die Parameter die Defaultwerte maxsize = 128 und typed = False verwendet. Falls maxsize auf None gesetzt wird, werden die LRU-Eigenschaften disabled und der Cache kann ungebunden wachsen. Wir demonstrieren dies im folgenden Beispiel:
import functools
@functools.lru_cache(maxsize=None)
def f(x):
return x
for i in range(1000):
f(i)
print(f.cache_info())
An der Ausgabe können wir erkennen, dass der Cache auf 1000 Elemente angestiegen ist.
Ruft man den Dekorateur entweder ohne Argumente oder mit der Zuweisung maxsize=128 auf, so können wir an der Ausgabe sehen, dass der Cache auf 128 begrenzt ist:
import functools
@functools.lru_cache(maxsize=128)
def f(x):
return x
print(f.cache_info())
Falls typed auf True gesetzt ist, werden Argumente von verschiedenem Type separat gecashed. So werden dann z.B. f(3.0) und f(3) als verschiedene Aufrufe betrachtet. Die Argumente der dekorierten Funktion müssen hash-bar sein. Die zugrundeliegende Funktion kann man mit f.__wrapped__ ansprechen.
@functools.lru_cache(typed=True)
def g(x):
return x
g(1)
g(1.0)
g.cache_info()
Weitere Beispiele mit Dekorateuren Überprüfung von Argumenten durch Dekorateure In unserem Kapitel über rekursive Funktionen hatten wir die Fakultätsfunktion eingeführt. Dabei wollten wir die Funktion so einfach wie möglich halten. Hätten wir die Argumente der Fakultätsfunktion auf Plausibilität geprüft, hätten wir die zugrunde liegende Idee verschleiert und der Kern des Algorithmus wäre nicht mehr so erkenntlich gewesen. So darf die Funktion keinesfalls mit negativen Werten oder Fließkommazahlen, also float-Werten, aufgerufen werden. In beiden Fällen kommt es zu einer endlosen Rekursion, die allerdings glücklicherweise durch den endlichen Rekursionsstack von Python mit einem RuntimeError abgebrochen wird:
RuntimeError: maximum recursion depth exceeded in comparison
Das folgende Programm benutzt eine Dekorateur-Funktion um sicherzustellen, dass es sich bei dem verwendeten Argument, um eine positive ganze Zahl handelt:
def Argument_Test_natürliche_Zahl(f):
def Helper(x):
if type(x) == int and x > 0:
return f(x)
else:
raise Exception("Argument ist keine ganze Zahl")
return Helper
@Argument_Test_natürliche_Zahl
def Fakultät(n):
if n == 1:
return 1
else:
return n * Fakultät(n-1)
for i in range(1,10):
print(i, Fakultät(i))
print(Fakultät(-1))
def Aufruf_Zähler(func):
def Helper(*args, **kwargs):
Helper.calls += 1
return func(*args, **kwargs)
Helper.calls = 0
Helper.__name__= func.__name__
return Helper
@Aufruf_Zähler
def Nachfg(x):
return x + 1
print(Nachfg.calls)
for i in range(10):
print(Nachfg(i))
print(Nachfg.calls)
class Memoize:
def __init__(self, fn):
self.fn = fn
self.memo = {}
def __call__(self, *args):
if args not in self.memo:
self.memo[args] = self.fn(*args)
return self.memo[args]
@Memoize
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
print(fib(40))
Da wir ein Wörterbuch verwenden, können wir keine veränderlichen Argumente verwenden, d. H. Die Argumente müssen unveränderlich sein.
Übung
Unsere Übung ist ein altes Rätsel aus dem Jahr 1612. Der französische Jesuit Claude-Gaspar Bachet hat es formuliert. Wir müssen Mengen (z. B. Zucker oder Mehl) von 1 bis 40 Pfund wiegen. Was ist die geringste Anzahl von Gewichten, die auf einer Waage verwendet werden können, um eine dieser Größen zu bestimmen?
Die erste Idee könnte sein, Gewichte von 1, 2, 4, 8, 16 und 32 Pfund zu verwenden. Dies ist eine minimale Zahl, wenn wir uns darauf beschränken, Gewichte auf eine Seite zu legen und das Zeug, z. der Zucker auf der anderen Seite. Es ist jedoch möglich, Gewichte auf beide Pfannen der Waage zu legen. Jetzt brauchen wir nur vier Gewichte, d. H. 1, 3, 9, 27
Schreiben Sie eine Python-Funktion wiegen (), die die benötigten Gewichte und deren Verteilung auf den Pfannen berechnet, um eine beliebige Menge von 1 bis 40 zu wiegen.
Lösung
Wir benötigen die Funktion linear_combination () aus unserem Kapitel Lineare Kombinationen.
def Faktoren_Menge():
for i in [-1, 0, 1]:
for j in [-1, 0, 1]:
for k in [-1, 0, 1]:
for l in [-1, 0, 1]:
yield (i, j, k, l)
def memoize(f):
Ergebnisse = {}
def Helper(n):
if n not in Ergebnisse:
Ergebnisse[n] = f(n)
return Ergebnisse[n]
return Helper
@memoize
def linearkombination(n):
""" gibt das Tupel zurück (i,j,k,l) welches die Gleichung
n = i*1 + j*3 + k*9 + l*27 erfüllt """
Gewichte = (1, 3, 9, 27)
for Faktoren in Faktoren_Menge():
sum = 0
for i in range(len(Faktoren)):
sum += Faktoren[i] * Gewichte[i]
if sum == n:
return Faktoren
Damit ist es einfach, unsere Funktion gewogen () zu schreiben.
def wiegen(pfund):
gewichte = (1, 3, 9, 27)
skalare = linearkombination(pfund)
links = ""
rechts = ""
for i in range(len(skalare)):
if skalare[i] == -1:
links += str(gewichte[i]) + " "
elif skalare[i] == 1:
rechts += str(gewichte[i]) + " "
return (links,rechts)
for i in [2, 3, 4, 7, 8, 9, 20, 40]:
waagschale = wiegen(i)
print("Linke Waagschale: " + str(i) + " plus " + waagschale[0])
print("Rechte Waagschale: " + waagschale[1] + "\n")

 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen

